题目内容
已知a,b,c是正整数,且抛物线y=ax2+bx+c与x轴有两个不同的交点A,B,若A,B到原点的距离都小于1,则a+b+c的最小值为
- A.8
- B.9
- C.10
- D.11
D
分析:先根据方程ax2+bx+c=0有两个相异根都在(-1,0)中可得到,a-b+c>0, <1,且b2-4ac>0,再由不等式的基本性质可求出a的取值范围,再根据a、b、c之间的关系即可求解.
<1,且b2-4ac>0,再由不等式的基本性质可求出a的取值范围,再根据a、b、c之间的关系即可求解.
解答:据题意得,方程ax2+bx+c=0有两个相异根,都在(-1,0)中,
故当x=-1时,y>0,则a-b+c>0,一元二次方程ax2+bx+c=0的两根 =x1x2<1,且b2-4ac>0①,
=x1x2<1,且b2-4ac>0①,
∵a,b,c都为正整数,a-b+c>0,
∴a-b+c≥1②,且a>c③,
由b2-4ac>0,得到b2>4ac,即b>2 ,
,
∴a+c≥b+1>2 +1,即(
+1,即( -
- )2>1,
)2>1,
由③得, >
> +1,故a>4,
+1,故a>4,
又b>2 ≥2
≥2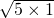 >4,
>4,
故分别取a、b、c的最小整数5、5、1,经检验,符合题意,
则a+b+c的最小值为11.
故选D.
点评:本题考查的是抛物线与x轴的交点问题,基本不等式的运用,以及根的判别式,由a-b+c>0, <1,且b2-4ac>0得到关于a、b、c的关系式是解答此题的关键.
<1,且b2-4ac>0得到关于a、b、c的关系式是解答此题的关键.
分析:先根据方程ax2+bx+c=0有两个相异根都在(-1,0)中可得到,a-b+c>0,
 <1,且b2-4ac>0,再由不等式的基本性质可求出a的取值范围,再根据a、b、c之间的关系即可求解.
<1,且b2-4ac>0,再由不等式的基本性质可求出a的取值范围,再根据a、b、c之间的关系即可求解.解答:据题意得,方程ax2+bx+c=0有两个相异根,都在(-1,0)中,
故当x=-1时,y>0,则a-b+c>0,一元二次方程ax2+bx+c=0的两根
 =x1x2<1,且b2-4ac>0①,
=x1x2<1,且b2-4ac>0①,∵a,b,c都为正整数,a-b+c>0,
∴a-b+c≥1②,且a>c③,
由b2-4ac>0,得到b2>4ac,即b>2
 ,
,∴a+c≥b+1>2
 +1,即(
+1,即( -
- )2>1,
)2>1,由③得,
 >
> +1,故a>4,
+1,故a>4,又b>2
 ≥2
≥2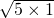 >4,
>4,故分别取a、b、c的最小整数5、5、1,经检验,符合题意,
则a+b+c的最小值为11.
故选D.
点评:本题考查的是抛物线与x轴的交点问题,基本不等式的运用,以及根的判别式,由a-b+c>0,
 <1,且b2-4ac>0得到关于a、b、c的关系式是解答此题的关键.
<1,且b2-4ac>0得到关于a、b、c的关系式是解答此题的关键. 
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
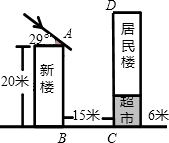 夹角为29°.(参考数据:sin29°≈0.48;cos29°≈0.87;tan29°≈0.55)
夹角为29°.(参考数据:sin29°≈0.48;cos29°≈0.87;tan29°≈0.55)