题目内容
某厂今年一月份新产品研发资金为a元，以后每月新产品的研发资金与上月相比增长率都是x，则该厂今年前三个月份新产品的研发资金总和为 ．
考点：由实际问题抽象出一元二次方程
专题：
分析：由一月份新产品的研发资金为a元，根据题意可以得到2月份研发资金为a×（1+x），而三月份在2月份的基础上又增长了x，那么三月份的研发资金也可以用x表示出来即可．
解答：解：∵一月份新产品的研发资金为a元，
2月份起，每月新产品的研发资金与上月相比增长率都是x，
∴2月份研发资金为a×（1+x），
∴三月份的研发资金为a×（1+x）×（1+x）=a（1+x）2．
故答案为：a（1+x）2．
2月份起，每月新产品的研发资金与上月相比增长率都是x，
∴2月份研发资金为a×（1+x），
∴三月份的研发资金为a×（1+x）×（1+x）=a（1+x）2．
故答案为：a（1+x）2．
点评：此题主要考查了根据实际问题抽象出一元二次方程，此题是平均增长率的问题，可以用公式a（1±x）2=b来解题．
练习册系列答案
相关题目
下列方程中是一元二次方程的是（ ）
| A、（x+1）2-1=x2+4 | ||
| B、3x2-2xy-5y2=0 | ||
| C、（x+1）（x-1）=0 | ||
D、x-
|
“井底之蛙”要爬出来，他每小时爬上5米，休息一小时又滑下3米，若井深11米，则它爬出井来需要（ ）小时．
| A、5 | B、6 | C、7 | D、8 |
2015年南箐小学的营养餐费用大约用去1370000元，将1370000用科学记数法表示为（ ）
| A、137×104 |
| B、13.7×105 |
| C、1.37×106 |
| D、1.37×104 |
一个几何体由若干大小相同的小正方形搭成，从正面、上面看到的这个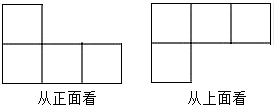
几何体的形状图如图所示．搭成这个几何体用到的小正方形的个数最多是（ ）
几何体的形状图如图所示．搭成这个几何体用到的小正方形的个数最多是（ ）| A、4个 | B、5个 | C、6个 | D、7个 |
如图，在不等边△ABC中，PM⊥AB于点M，PN⊥AC于点N，且PM=PN，Q在AC上，PQ=QA，MP=3，△AMP的面积是6，下列结论：①AM＜PQ+QN，②QP∥AM，③△BMP≌△PQC，④∠QPC+∠MPB=90°，⑤△PQN的周长是7，其中正确的有（ ）个．若关于x的函数y=kx2+2x-1与x轴只有一个交点，则实数k的值为（ ）
| A、-1 | B、-2 | C、1 | D、2 |