题目内容
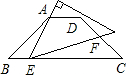 在等腰梯形ABCD中,AD∥BC,BC=4AD,AD=
在等腰梯形ABCD中,AD∥BC,BC=4AD,AD=| 2 |
分析:首先理解题意,得出此题应该分两种情况进行分析,分别是AB=AE,AB=BE,从而得到最后答案.
解答: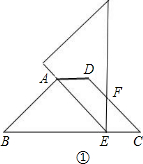 解:根据已知条件可得,
解:根据已知条件可得,
AB=(BC-AD)÷2÷cosB=3.
①当AB=AE时,如图,
∠B=45°,∠AEB=45°,AE=AB=3,
则在Rt△ABE中,BE=
=3
,
故EC=4
-3
=
.
易得△FEC为等腰直角三角形,
故FC=
=2.
②当AB=BE时,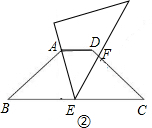
∵∠B+∠BAE=45°+∠CEF,∠B=45°,
∴∠CEF=∠EAB,
∵∠B=∠C,
∴△ABE∽△ECF,
∵
=
,
∴
=
,
∴CF=4
-3;
△ABE∽△FCE,
∴
=
,
∴
=
CF=4
-3,
故答案为:2或4
-3.
 解:根据已知条件可得,
解:根据已知条件可得,AB=(BC-AD)÷2÷cosB=3.
①当AB=AE时,如图,
∠B=45°,∠AEB=45°,AE=AB=3,
则在Rt△ABE中,BE=
| 32+32 |
| 2 |
故EC=4
| 2 |
| 2 |
| 2 |
易得△FEC为等腰直角三角形,
故FC=
(
|
②当AB=BE时,

∵∠B+∠BAE=45°+∠CEF,∠B=45°,
∴∠CEF=∠EAB,
∵∠B=∠C,
∴△ABE∽△ECF,
∵
| AB |
| CE |
| BE |
| CF |
∴
| 3 | ||
4
|
| 3 |
| CF |
∴CF=4
| 2 |
△ABE∽△FCE,
∴
| AB |
| FC |
| EB |
| CE |
∴
| 3 |
| CF |
| 3 | ||
4
|
CF=4
| 2 |
故答案为:2或4
| 2 |
点评:此题主要考查了等腰梯形的性质,以及等腰直角三角形的性质,综合性较强.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
 25、如图所示,在等腰梯形ABCD中,AD∥BC,AB=CD,点P为BC边上任意一点,且
25、如图所示,在等腰梯形ABCD中,AD∥BC,AB=CD,点P为BC边上任意一点,且 24、已知:如图,在等腰梯形ABCD中,AD∥BC,AB=DC,点E为边BC上一点,且AE=DC.
24、已知:如图,在等腰梯形ABCD中,AD∥BC,AB=DC,点E为边BC上一点,且AE=DC.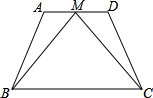 如图,在等腰梯形ABCD中,AD∥BC,M是AD的中点,MB=MC吗?为什么?
如图,在等腰梯形ABCD中,AD∥BC,M是AD的中点,MB=MC吗?为什么? 如图,在等腰梯形ABCD中,AD∥BC,AB=CD,AC⊥BD,垂足为O,过D作DE∥AC交BC的延长线于E.
如图,在等腰梯形ABCD中,AD∥BC,AB=CD,AC⊥BD,垂足为O,过D作DE∥AC交BC的延长线于E.