题目内容
小明到服装店参加社会实践活动,服装店经理让小明帮助解决以下问题:
服装店准备购进甲乙两种服装,甲种每件进价80元,售价120元;乙种每件进价60元,售价90元.计划购进两种服装共100件,其中甲种服装不少于65件。
(1)若购进这100件服装的费用不得超过7500,则甲种服装最多购进多少件?
(2)在(1)的条件下,该服装店对甲种服装以每件优惠a(0<a<20)元的价格进行优惠促销活动,乙种服装价格不变,那么该服装店应如何调整进货方案才能获得最大利润?
解:(1)设购进甲种服装x件,由题意可知:
80x+60(100-x)≤7500 解得:x≤75
答:甲种服装最多购进75件.
(2)设总利润为w元,因为甲种服装不少于65件,所以65≤x≤75
W=(40-a)x+30(100-x)=(10-a)x+3000
方案1:当0<a<10时,10-a>0,w随x的增大而增大
所以当x=75时,w有最大值,则购进甲种服装75件,乙种服装25件;
方案2:当a=10时,所有方案获利相同,所以按哪种方案进货都可以;
方案3:当10<a<20时,10-a<0,w随x的增大而减小
所以当x=65时,w有最大值,则购进甲种服装65件,乙种服装35件。

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目
 ,求m的値:
,求m的値: 线AC与直线PQ交于点D,求:
线AC与直线PQ交于点D,求: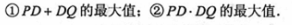
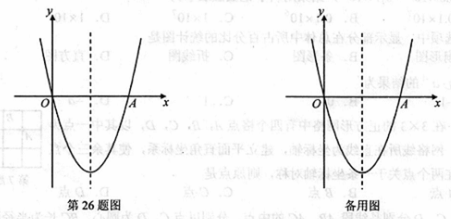
 ,则
,则 的值为 .
的值为 . 的根,则三角形的周长为
的根,则三角形的周长为 =
=  的倒数是
的倒数是 B.
B. D.
D.
 ,则图中阴影部分面积是 .
,则图中阴影部分面积是 .