Question

【题目】某工厂现有甲种原料360千克，乙种原料290千克，计划利用这两种原料生产A、B两种产品共50件．已知生产一件A种产品，需用甲种原料9千克、乙种原料3千克，可获利润700元；生产一件B种产品，需用甲种原料4千克、乙种原料10千克，可获利润1200元．设生产A种产品的生产件数为x，A、B两种产品所获总利润为y（元）．
（1）试写出y与x之间的函数关系式；
（2）求出自变量x的取值范围；
（3）利用函数的性质说明哪种生产方案获总利润最大？最大利润是多少？

Answer 1

【答案】
（1）解：设生产A种产品x件，则生产B种产品（50﹣x）件，

由题意得：y=700x+1200（50﹣x）=﹣500x+60000，

即y与x之间的函数关系式为y=﹣500x+60000

（2）解：由题意得 ，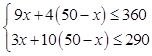

解得30≤x≤32．

∵x为整数，

∴整数x=30，31或32

（3）解：∵y=﹣500x+60000，﹣500＜0，

∴y随x的增大而减小，

∵x=30，31或32，

∴当x=30时，y有最大值为﹣500×30+60000=45000．

即生产A种产品30件，B种产品20件时，总利润最大，最大利润是45000元

【解析】（1）由于用这两种原料生产A、B两种产品共50件，设生产A种产品x件，那么生产B种产品（50﹣x）件．由A产品每件获利700元，B产品每件获利1200元，根据总利润=700×A种产品数量+1200×B种产品数量即可得到y与x之间的函数关系式；（2）关系式为：A种产品需要甲种原料数量+B种产品需要甲种原料数量≤360；A种产品需要乙种原料数量+B种产品需要乙种原料数量≤290，把相关数值代入得到不等式组，解不等式组即可得到自变量x的取值范围；（3）根据（1）中所求的y与x之间的函数关系式，利用一次函数的增减性和（2）得到的取值范围即可求得最大利润．
【考点精析】掌握一元一次不等式组的应用是解答本题的根本，需要知道1、审：分析题意，找出不等关系；2、设：设未知数；3、列：列出不等式组；4、解：解不等式组；5、检验：从不等式组的解集中找出符合题意的答案；6、答：写出问题答案．