题目内容
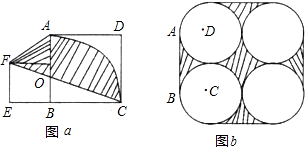
如图,在边长为3cm的正方形中,⊙P与⊙Q相外切,且⊙P分别与DA、DC边相切,⊙Q分别与BA、BC边相切,则圆心距PQ为________.
(6-3 )cm
)cm
分析:连接BD,则圆心P、Q在BD上,设⊙P与正方形的切点为H、G,设大圆的半径为R,小圆的半径为r,利用切线长定理和勾股定理求出DP,BQ,DB的长,进而求出PQ的长.
解答:连接BD,则圆心P、Q在BD上,设⊙P与正方形的切点为H、G,设大圆的半径为R,小圆的半径为r,
∵且⊙P分别与DA、DC边相切,
∴PG⊥AD、PH⊥DC,
又∵PG=PH=R,
∴四边形GPHD为正方形,
∴DP= PH=
PH= R,
R,
同理,BQ= r,
r,
∵AB=AD=3cm,
∴DB= =3
=3 ,
,
∴DP+PQ+BQ=BD=3 ,
,
即: r+(r+R)+
r+(r+R)+ R=3
R=3 ,
,
∴( +1)(r+R)=3
+1)(r+R)=3 ,
,
PQ= =(6-3
=(6-3 )cm.
)cm.
故答案为:(6-3 )cm.
)cm.
点评:此题主要考查了相切两圆的性质和正方形的性质以及切线长定理,解题的关键是圆心距PQ=两半径之和.
 )cm
)cm分析:连接BD,则圆心P、Q在BD上,设⊙P与正方形的切点为H、G,设大圆的半径为R,小圆的半径为r,利用切线长定理和勾股定理求出DP,BQ,DB的长,进而求出PQ的长.
解答:连接BD,则圆心P、Q在BD上,设⊙P与正方形的切点为H、G,设大圆的半径为R,小圆的半径为r,
∵且⊙P分别与DA、DC边相切,
∴PG⊥AD、PH⊥DC,
又∵PG=PH=R,
∴四边形GPHD为正方形,

∴DP=
 PH=
PH= R,
R,同理,BQ=
 r,
r,∵AB=AD=3cm,
∴DB=
 =3
=3 ,
,∴DP+PQ+BQ=BD=3
 ,
,即:
 r+(r+R)+
r+(r+R)+ R=3
R=3 ,
,∴(
 +1)(r+R)=3
+1)(r+R)=3 ,
,PQ=
 =(6-3
=(6-3 )cm.
)cm.故答案为:(6-3
 )cm.
)cm.点评:此题主要考查了相切两圆的性质和正方形的性质以及切线长定理,解题的关键是圆心距PQ=两半径之和.

练习册系列答案
相关题目