题目内容
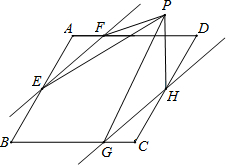 如图,在边长为4的菱形ABCD中,∠B=60°,点E、G、H、F分别在AB、BC、CD、AD上,且AF=CG=1,BE=DH=2,点P是直线EF、GH之间任意一点,连接PE、PF、PG、PH,则△PEF和△PGH的面积和等于
如图,在边长为4的菱形ABCD中,∠B=60°,点E、G、H、F分别在AB、BC、CD、AD上,且AF=CG=1,BE=DH=2,点P是直线EF、GH之间任意一点,连接PE、PF、PG、PH,则△PEF和△PGH的面积和等于
- A.4
- B.

- C.

- D.

B
分析:延长FE交CB的延长线于W,过E作EM⊥AD交DA延长线于M,过F作FN⊥CD于N,过A作AR⊥BC于R,连接FH、EG,求出平行四边形EFHG,求出菱形面积、△AEF、△CGH、△FHD、△EGB的面积,即可求出答案.
解答: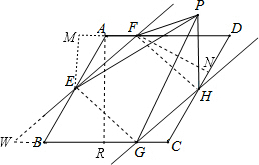
解:延长FE交CB的延长线于W,过E作EM⊥AD交DA延长线于M,过F作FN⊥CD于N,过A作AR⊥BC于R,连接FH、EG,
则∠M=∠FND=∠ARB=90°,
∵AB=4,∠B=60°,
∴∠BAR=30°,
∴BR=2,AR=2 ,
,
∵四边形ABCD是菱形,
∴AD∥BC,∠A=∠C,AB=AD=CB=4,
∵BE=CH=4,
∴AE=DH=2,
在△AEF和△CHG中
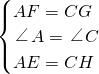 ,
,
∴△AEF≌△CHG(SAS),
∴EF=GH,∠AFE=∠HGC,
∵AD∥BC,
∴∠AFE=∠W,
∴∠W=∠HGC,
∴EF∥GH,
∵EF=GH,
∴四边形EFHG是平行四边形,
∴△PEF和△PGH的面积和S= EF×hEF+
EF×hEF+ GH×hGH=
GH×hGH= S平行四边形EFHG;
S平行四边形EFHG;
∵四边形ABCD是菱形,
∴AD∥BC,AC⊥BD,
∵∠B=60°,
∴∠B=∠MAE=60°,
∵∠M=90°
∴∠MEA=30°,
∵AB=4,BE=2,
∴AE=2,
∴AM= AE=1,
AE=1,
由勾股定理得:ME= ,
,
即△AEF的面积是S1= ×AF×ME=
×AF×ME= ×1×
×1× =
=
 ,
,
同理可得△CHG的面积S2=
 ,
,
∵四边形ABCD是菱形,∠B=60°,
∴∠D=∠B=60°,
∵∠FND=90°,
∴∠DFN=30°,
∴DN= DF=
DF= ×(4-1)=
×(4-1)= ,
,
由勾股定理得:FN=
 ,
,
∴△FHD的面积S3= DH×FN=
DH×FN= ×(4-2)×
×(4-2)×
 =
=
 ,
,
同理可得△BEG的面积S4=
 ,
,
∴平行四边形EFHG的面积是S菱形ABCD-S1-S2-S3-S4=4×2 -
-
 -
-
 -
-
 -
-
 =4
=4 ,
,
即△PEF和△PGH的面积和是 S平行四边形EFHG=2
S平行四边形EFHG=2 ,
,
故选B.
点评:本题考查了菱形的面积,平行四边形的性质和判定,全等三角形的性质和判定,平行线的性质和判定,三角形的内角和定理,含30度角的直角三角形性质,勾股定理等知识点的综合运用,本题综合性比较强,难度偏大.
分析:延长FE交CB的延长线于W,过E作EM⊥AD交DA延长线于M,过F作FN⊥CD于N,过A作AR⊥BC于R,连接FH、EG,求出平行四边形EFHG,求出菱形面积、△AEF、△CGH、△FHD、△EGB的面积,即可求出答案.
解答:

解:延长FE交CB的延长线于W,过E作EM⊥AD交DA延长线于M,过F作FN⊥CD于N,过A作AR⊥BC于R,连接FH、EG,
则∠M=∠FND=∠ARB=90°,
∵AB=4,∠B=60°,
∴∠BAR=30°,
∴BR=2,AR=2
 ,
,∵四边形ABCD是菱形,
∴AD∥BC,∠A=∠C,AB=AD=CB=4,
∵BE=CH=4,
∴AE=DH=2,
在△AEF和△CHG中
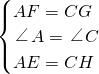 ,
,∴△AEF≌△CHG(SAS),
∴EF=GH,∠AFE=∠HGC,
∵AD∥BC,
∴∠AFE=∠W,
∴∠W=∠HGC,
∴EF∥GH,
∵EF=GH,
∴四边形EFHG是平行四边形,
∴△PEF和△PGH的面积和S=
 EF×hEF+
EF×hEF+ GH×hGH=
GH×hGH= S平行四边形EFHG;
S平行四边形EFHG;∵四边形ABCD是菱形,
∴AD∥BC,AC⊥BD,
∵∠B=60°,
∴∠B=∠MAE=60°,
∵∠M=90°
∴∠MEA=30°,
∵AB=4,BE=2,
∴AE=2,
∴AM=
 AE=1,
AE=1,由勾股定理得:ME=
 ,
,即△AEF的面积是S1=
 ×AF×ME=
×AF×ME= ×1×
×1× =
=
 ,
,同理可得△CHG的面积S2=

 ,
,∵四边形ABCD是菱形,∠B=60°,
∴∠D=∠B=60°,
∵∠FND=90°,
∴∠DFN=30°,
∴DN=
 DF=
DF= ×(4-1)=
×(4-1)= ,
,由勾股定理得:FN=

 ,
,∴△FHD的面积S3=
 DH×FN=
DH×FN= ×(4-2)×
×(4-2)×
 =
=
 ,
,同理可得△BEG的面积S4=

 ,
,∴平行四边形EFHG的面积是S菱形ABCD-S1-S2-S3-S4=4×2
 -
-
 -
-
 -
-
 -
-
 =4
=4 ,
,即△PEF和△PGH的面积和是
 S平行四边形EFHG=2
S平行四边形EFHG=2 ,
,故选B.
点评:本题考查了菱形的面积,平行四边形的性质和判定,全等三角形的性质和判定,平行线的性质和判定,三角形的内角和定理,含30度角的直角三角形性质,勾股定理等知识点的综合运用,本题综合性比较强,难度偏大.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
