题目内容
已知关于x的一元二次方程x2-mx+2m-1=0的两个实数根的平方和为7,那么m的值是
- A.5
- B.-1
- C.5或-1
- D.-5或1
B
分析:因为方程x2-mx+2m-1=0有两实根,所以△≥0;然后把两实根的平方和变形为两根之积或两根之和的形式.根据这两种情况确定m的取值范围.
解答:∵方程x2-mx+2m-1=0有两实根,∴△≥0;
即(-m)2-4(2m-1)=m2-8m+4≥0,
解得m≥ 或m≤
或m≤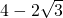 .
.
设原方程的两根为α、β,则α+β=m,αβ=2m-1.
α2+β2=α2+β2+2αβ-2αβ
=(α+β)2-2αβ
=m2-2(2m-1)
=m2-4m+2=7.
即m2-4m-5=0.
解得m=-1或m=5
∵m=5≤ ,∴m=5(舍去)
,∴m=5(舍去)
∴m=-1.故选B
点评:本题考查一元二次方程根与系数的关系及根的判别式,同时考查代数式变形与不等式的解法.
分析:因为方程x2-mx+2m-1=0有两实根,所以△≥0;然后把两实根的平方和变形为两根之积或两根之和的形式.根据这两种情况确定m的取值范围.
解答:∵方程x2-mx+2m-1=0有两实根,∴△≥0;
即(-m)2-4(2m-1)=m2-8m+4≥0,
解得m≥
 或m≤
或m≤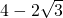 .
.设原方程的两根为α、β,则α+β=m,αβ=2m-1.
α2+β2=α2+β2+2αβ-2αβ
=(α+β)2-2αβ
=m2-2(2m-1)
=m2-4m+2=7.
即m2-4m-5=0.
解得m=-1或m=5
∵m=5≤
 ,∴m=5(舍去)
,∴m=5(舍去)∴m=-1.故选B
点评:本题考查一元二次方程根与系数的关系及根的判别式,同时考查代数式变形与不等式的解法.

练习册系列答案
相关题目
已知关于x的一元二次x2-6x+k+1=0的两个实数根x1,x2,
+
=1,则k的值是( )
| 1 |
| x1 |
| 1 |
| x2 |
| A、8 | B、-7 | C、6 | D、5 |
 .
. .
.