题目内容
 已知:如图,菱形ABCD中,对角线AC,BD相交于点O,且AC=12cm,BD=16cm.点P从点B出发,沿BA方向匀速运动,速度为1cm/s;同时,直线EF从点D出发,沿DB方向匀速运动,速度为1cm/s,EF⊥BD,且与AD,BD,CD分别交于点E,Q,F;当直线EF停止运动时,点P也停止运动.连接PF,设运动时间为t(s)(0<t<8).解答下列问题:
已知:如图,菱形ABCD中,对角线AC,BD相交于点O,且AC=12cm,BD=16cm.点P从点B出发,沿BA方向匀速运动,速度为1cm/s;同时,直线EF从点D出发,沿DB方向匀速运动,速度为1cm/s,EF⊥BD,且与AD,BD,CD分别交于点E,Q,F;当直线EF停止运动时,点P也停止运动.连接PF,设运动时间为t(s)(0<t<8).解答下列问题:(1)当t为何值时,四边形APFD是平行四边形?
(2)设四边形APFE的面积为y(cm2),求y与t之间的函数关系式;
(3)是否存在某一时刻t,使S四边形APFE:S菱形ABCD=17:40?若存在,求出t的值,并求出此时P,E两点间的距离;若不存在,请说明理由.
考点:四边形综合题,相似三角形的性质
专题:几何综合题,压轴题
分析:(1))由四边形ABCD是菱形,OA=
AC,OB=
BD.在Rt△AOB中,运用勾股定理求出AB=10.再由△DFQ∽△DCO.得出
=
.求出DF.由AP=DF.求出t.
(2)过点C作CG⊥AB于点G,由S菱形ABCD=AB•CG=
AC•BD,求出CG.据S梯形APFD=
(AP+DF)•CG.S△EFD=
EF•QD.得出y与t之间的函数关系式;
(3)过点C作CG⊥AB于点G,由S菱形ABCD=AB•CG,求出CG,由S四边形APFE:S菱形ABCD=17:40,求出t,再由△PBN∽△ABO,求得PN,BN,据线段关系求出EM,PM再由勾股定理求出PE.
| 1 |
| 2 |
| 1 |
| 2 |
| DF |
| DC |
| QD |
| OD |
(2)过点C作CG⊥AB于点G,由S菱形ABCD=AB•CG=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
(3)过点C作CG⊥AB于点G,由S菱形ABCD=AB•CG,求出CG,由S四边形APFE:S菱形ABCD=17:40,求出t,再由△PBN∽△ABO,求得PN,BN,据线段关系求出EM,PM再由勾股定理求出PE.
解答:解:(1)∵四边形ABCD是菱形,
∴AB∥CD,AC⊥BD,OA=OC=
AC=6,OB=OD=
BD=8.
在Rt△AOB中,AB=
=10.
∵EF⊥BD,
∴∠FQD=∠COD=90°.
又∵∠FDQ=∠CDO,
∴△DFQ∽△DCO.
∴
=
.
即
=
,
∴DF=
t.
∵四边形APFD是平行四边形,
∴AP=DF.
即10-t=
t,
解这个方程,得t=
.
∴当t=
s时,四边形APFD是平行四边形.
(2)如图,过点C作CG⊥AB于点G,
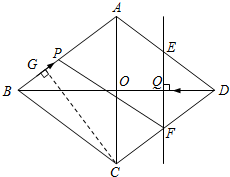
∵S菱形ABCD=AB•CG=
AC•BD,
即10•CG=
×12×16,
∴CG=
.
∴S梯形APFD=
(AP+DF)•CG
=
(10-t+
t)•
=
t+48.
∵△DFQ∽△DCO,
∴
=
.
即
=
,
∴QF=
t.
同理,EQ=
t.
∴EF=QF+EQ=
t.
∴S△EFD=
EF•QD=
×
t×t=
t2.
∴y=(
t+48)-
t2=-
t2+
t+48.
(3)如图,过点P作PM⊥EF于点M,PN⊥BD于点N,
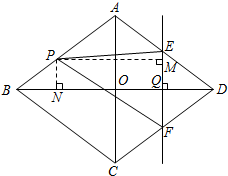
若S四边形APFE:S菱形ABCD=17:40,
则-
t2+
t+48=
×96,
即5t2-8t-48=0,
解这个方程,得t1=4,t2=-
(舍去)
过点P作PM⊥EF于点M,PN⊥BD于点N,
当t=4时,
∵△PBN∽△ABO,
∴
=
=
,即
=
=
.
∴PN=
,BN=
.
∴EM=EQ-MQ=3-
=
.
PM=BD-BN-DQ=16-
-4=
.
在Rt△PME中,
PE=
=
=
(cm).
∴AB∥CD,AC⊥BD,OA=OC=
| 1 |
| 2 |
| 1 |
| 2 |
在Rt△AOB中,AB=
| 62+82 |
∵EF⊥BD,
∴∠FQD=∠COD=90°.
又∵∠FDQ=∠CDO,
∴△DFQ∽△DCO.
∴
| DF |
| DC |
| QD |
| OD |
即
| DF |
| 10 |
| t |
| 8 |
∴DF=
| 5 |
| 4 |
∵四边形APFD是平行四边形,
∴AP=DF.
即10-t=
| 5 |
| 4 |
解这个方程,得t=
| 40 |
| 9 |
∴当t=
| 40 |
| 9 |
(2)如图,过点C作CG⊥AB于点G,

∵S菱形ABCD=AB•CG=
| 1 |
| 2 |
即10•CG=
| 1 |
| 2 |
∴CG=
| 48 |
| 5 |
∴S梯形APFD=
| 1 |
| 2 |
=
| 1 |
| 2 |
| 5 |
| 4 |
| 48 |
| 5 |
| 6 |
| 5 |
∵△DFQ∽△DCO,
∴
| QD |
| OD |
| QF |
| OC |
即
| t |
| 8 |
| QF |
| 6 |
∴QF=
| 3 |
| 4 |
同理,EQ=
| 3 |
| 4 |
∴EF=QF+EQ=
| 3 |
| 2 |
∴S△EFD=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 3 |
| 4 |
∴y=(
| 6 |
| 5 |
| 3 |
| 4 |
| 3 |
| 4 |
| 6 |
| 5 |
(3)如图,过点P作PM⊥EF于点M,PN⊥BD于点N,

若S四边形APFE:S菱形ABCD=17:40,
则-
| 3 |
| 4 |
| 6 |
| 5 |
| 17 |
| 40 |
即5t2-8t-48=0,
解这个方程,得t1=4,t2=-
| 12 |
| 5 |
过点P作PM⊥EF于点M,PN⊥BD于点N,
当t=4时,
∵△PBN∽△ABO,
∴
| PN |
| AO |
| PB |
| AB |
| BN |
| BO |
| PN |
| 6 |
| 4 |
| 10 |
| BN |
| 8 |
∴PN=
| 12 |
| 5 |
| 16 |
| 5 |
∴EM=EQ-MQ=3-
| 12 |
| 5 |
| 3 |
| 5 |
PM=BD-BN-DQ=16-
| 16 |
| 5 |
| 44 |
| 5 |
在Rt△PME中,
PE=
| PM2+EM2 |
(
|
| ||
| 5 |
点评:本题主要考查了四边形的综合知识,解题的关键是根据三角形相似比求出相关线段.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
下列说法正确的是( )
| A、邻补角相等 |
| B、对顶角相等 |
| C、任意两角的补角相等 |
| D、任意两角的余角相等 |
 在平面直角坐标系中,△ABC的三个顶点坐标分别为A(-2,1),B(-4,5),C(-5,2).
在平面直角坐标系中,△ABC的三个顶点坐标分别为A(-2,1),B(-4,5),C(-5,2).
 如图,等腰梯形ABCD中,如果AD∥BC,BD平分∠ABC,AD=2,∠C=60°,则BC=
如图,等腰梯形ABCD中,如果AD∥BC,BD平分∠ABC,AD=2,∠C=60°,则BC=