Question

已知二次函数y＝x²－x＋c.

(1)若点A(－1，n)，B(2,2n－1)在二次函数y＝x²－x＋c的图象上，求此二次函数的最小值；

(2)若点D(x₁，y₁)，E(x₂，y₂)，P(m，m)(m＞0)在抛物线y＝x²－x＋c上，且D，E两点关于坐标原点成中心对称，连接PO，当2≤PO≤＋2时，试判断直线DE与抛物线y＝x²－x＋c＋的交点个数，并说明理由.

Answer 1

解：(1)法1：由题意得 　　　　　　　　　　　　　　　

解得 　　　　　　　　　　　　　　　　　　　　　　　　　　

法2：∵抛物线y＝x²－x＋c的对称轴是x＝，

且－(－1) ＝2－，∴A，B两点关于对称轴对称.

∴n＝2n－1 　　　　　　　　　　　　　　　　　　　　　　　　　　　　

∴n＝1，c＝－1.　　　　　　　　　　　　　　　　　　　　　　　　　　

∴有 y＝x²－x－1 　　　　　　　　　　　　　　　　　　　　　　　　

＝(x－)²－.

∴二次函数y＝x²－x－1的最小值是－.　　　　　　　　　　　　　　　

(2)∵点P(m，m)(m＞0)，

∴PO＝m.

∴2≤m≤＋2.

∴2≤m≤1＋.　　　　　　　　　　　　　　　　　　　　　　　　　

法1：∵点P(m，m)(m＞0)在二次函数y＝x²－x＋c的图象上，

∴m＝m²－m＋c，即c＝－m²＋2m.

∵开口向下，且对称轴m＝1，

∴当2≤m≤1＋时，

有 －1≤c≤0.(6分)

法2：∵2≤m≤1＋，

∴1≤m－1≤.

∴1≤(m－1)²≤2.

∵点P(m，m)(m＞0)在二次函数y＝x²－x＋c的图象上，

∴m＝m²－m＋c，即1－c＝(m－1)².

∴1≤1－c≤2.

∴－1≤c≤0.　　　　　　　　　　　　　　　　　　　　　　　　　　　

∵点D，E关于原点成中心对称，

法1：∴x₂＝－x₁，y₂＝－y₁.

∴

∴2y₁＝－2x₁，y₁＝－x₁.

设直线DE：y＝kx.

有 －x₁＝kx₁.

由题意，存在x₁≠x₂.

∴存在x₁，使x₁≠0.　　　　　　　　　　　　　　　　　　　　　　　　

∴k＝－1.

∴直线DE：y＝－x.　　　　　　　　　　　　　　　　　　　　　　　

法2：设直线DE：y＝kx.

则根据题意有 kx＝x²－x＋c，即x²－(k＋1)x＋c＝0.

∵－1≤c≤0，

∴(k＋1)²－4c≥0.

∴方程x²－(k＋1)x＋c＝0有实数根.　　　　　　　　　　　　　　　　　　

∵x₁＋x₂＝0，

∴k＋1＝0.

∴k＝－1.

∴直线DE：y＝－x.　　　　　　　　　　　　　　　　　　　　　　　

若 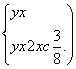则有 x²＋c＋＝0.

即 x²＝－c－.

①当－c－＝0时，即c＝－时，方程x²＝－c－有相同的实数根，

即直线y＝－x与抛物线y＝x²－x＋c＋有唯一交点；　　　　　　　　　　

②当－c－＞0时，即c＜－时，即－1≤c＜－时，

方程x²＝－c－有两个不同实数根，

即直线y＝－x与抛物线y＝x²－x＋c＋有两个不同的交点；　　　　　　　

③当－c－＜0时，即c＞－时，即－＜c≤0时，

方程x²＝－c－没有实数根，

即直线y＝－x与抛物线y＝x²－x＋c＋没有交点.