题目内容
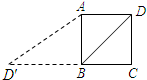如图所示，已知正方形ABCD的边长为1．如果将对角线BD绕着点B旋转后，点D落在CB的延长线上的D′点处，连接AD′，那么cot∠BAD′=分析：先根据勾股定理求出BD的长，再由图形旋转的性质得出D′B的长，由锐角三角函数的定义即可得出cot∠BAD′的值．
解答：解：∵四边形ABCD是正方形，AB=1，
∴BD=
=
=
，
∵BD绕着点B旋转后，点D落在CB的延长线上的D′点处，
∴D′B=BD=
，
∴cot∠BAD′=
=
=
．
故答案为：
．
∴BD=
| AB2+AD2 |
| 12+12 |
| 2 |
∵BD绕着点B旋转后，点D落在CB的延长线上的D′点处，
∴D′B=BD=
| 2 |
∴cot∠BAD′=
| AB |
| D′B |
| 1 | ||
|
| ||
| 2 |
故答案为：
| ||
| 2 |
点评：本题考查的是图形旋转的性质、正方形的性质及锐角三角函数的定义，熟知以上知识是解答此题的关键．
练习册系列答案
阅读快车系列答案
相关题目
33、如图所示，已知正方形ABCD，延长CB至E，连接AE，过点A作AF⊥AE交DC于F．
30、如图所示，已知正方形ABCD，E为BC上任意一点，延长AB至F，使BF=BE，AE的延长线交CF于G，
如图所示，已知正方形ABCD的面积是8平方厘米，正方形EFGH的面积是62平方厘米，BC落在EH上，△ACG的面积是4.9平方厘米，则△ABE的面积是（ ）
如图所示，已知正方形OABC的面积为9，点B在函数