题目内容
已知.a是不为1的有理数,我们把
称为a的差倒数.如:3的差倒数是
=-
,-2的差倒数是
=
.已知a1=2,a2是a1的差倒数,a3是a2的差倒数,a4是a3的差倒数,…,依此类推,则a2013=
.
| 1 |
| 1-a |
| 1 |
| 1-3 |
| 1 |
| 2 |
| 1 |
| 1-(-2) |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
分析:先依次计算出a2、a3、a4、a5,即可发现每3个数为一个循环,然后用2013除以3,即可得出答案.
解答:解:根据题意得:
a1=2,
a2=
=-1,
a3=
=
;
a4=
=2;
则三个数是一个周期,
则2013÷3=671,
故a2013=a3=
.
故答案为:
.
a1=2,
a2=
| 1 |
| 1-2 |
a3=
| 1 |
| 1-(-1) |
| 1 |
| 2 |
a4=
| 1 | ||
1-
|
则三个数是一个周期,
则2013÷3=671,
故a2013=a3=
| 1 |
| 2 |
故答案为:
| 1 |
| 2 |
点评:此题主要考查了数字的变化类,考查学生对倒数和数字变化类知识点的理解和掌握,解答此题的关键是依次计算出a2、a3、a4,找出数字变化的规律.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
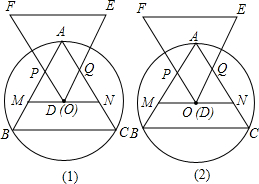 明理由;你能发现四边形APDQ的面积与△ABC的面积有何关系吗?为什么?
明理由;你能发现四边形APDQ的面积与△ABC的面积有何关系吗?为什么?