题目内容
6.在△ABC中,AB=AC=4,∠BAC=30°,以AC为一边作等边△ACD,连接BD.请画出图形,并直接写出△BCD的面积.分析 根据题意画出图形,进而利用勾股定理以及锐角三角函数关系求出BC的长,进而求出答案.
解答 解:如图所示: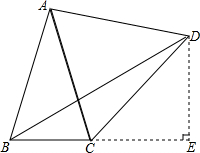
过点D作DE⊥BC延长线于点E,
∵AB=AC=4,∠BAC=30°,以AC为一边作等边△ACD,
∴∠BAD=90°,∠ABC=∠ACB=75°,AB=AD=DC=4,
∴∠ABD=∠ADB=45°,∠DBE=30°,∠DCE=45°,
∴DB=4$\sqrt{2}$,则DE=EC=2$\sqrt{2}$,BE=BDcos30°=2$\sqrt{6}$,
则BC=BE-EC=2$\sqrt{6}$-2$\sqrt{2}$,
则△BCD的面积为:$\frac{1}{2}$×2$\sqrt{2}$(2$\sqrt{6}$-2$\sqrt{2}$)=4$\sqrt{3}$-4.
如图所示:过点D作DE⊥BC延长线于点E,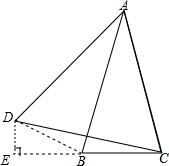
∵∠BAC=30°,△ACD是等边三角形,
∴∠DAB=30°,
∴AB垂直平分DC,
∴∠DBA=∠ABC=75°,BD=BC,
∴∠DBE=30°,
∴DE=$\frac{1}{2}$BD,
∴由(1)得:△BCD的面积为:$\frac{1}{2}$×$\frac{1}{2}$(2$\sqrt{6}$-2$\sqrt{2}$)(2$\sqrt{6}$-2$\sqrt{2}$)=8-4$\sqrt{3}$.
点评 此题主要考查了勾股定理以及等腰三角形的性质和锐角三角函数关系等知识,得出BC的长是解题关键.

练习册系列答案
相关题目
16.下列说法中正确的是( )
| A. | 掷两枚质地均匀的硬币,“两枚硬币都是正面朝上”这一事件发生的概率为$\frac{1}{2}$ | |
| B. | “对角线相等且相互垂直平分的四边形是正方形”这一事件是必然事件 | |
| C. | “同位角相等”这一事件是不可能事件 | |
| D. | “钝角三角形三条高所在直线的交点在三角形外部”这一事件是随机事件 |
17.下列因式分解正确的是( )
| A. | x2-4=(x+4)(x-4) | B. | x2+2x+1=x(x+2)+1 | C. | 3mx-6my=3m(x-6y) | D. | 2x+4=2(x+2) |
18.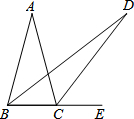 如图,在△ABC中,AB=AC,∠A=30°,E为BC延长线上一点,∠ABC与∠ACE的平分线相交于点D,则∠D的度数为( )
如图,在△ABC中,AB=AC,∠A=30°,E为BC延长线上一点,∠ABC与∠ACE的平分线相交于点D,则∠D的度数为( )
 如图,在△ABC中,AB=AC,∠A=30°,E为BC延长线上一点,∠ABC与∠ACE的平分线相交于点D,则∠D的度数为( )
如图,在△ABC中,AB=AC,∠A=30°,E为BC延长线上一点,∠ABC与∠ACE的平分线相交于点D,则∠D的度数为( )| A. | 15° | B. | 17.5° | C. | 20° | D. | 22.5° |
16.下列一元二次方程中,没有实数根的是( )
| A. | 4x2-5x+2=0 | B. | x2-6x+9=0 | C. | 5x2-4x-1=0 | D. | 3x2-4x+1=0 |