题目内容
已知四边形ABCD,AB∥CD,且AB=AC=AD=a,BC=b,且2a>b.求cos∠DBA的值.
【答案】分析:欲求∠DBA的余弦值,需将已知条件构建到一个直角三角形中求解;已知四边形ABCD中,AB=AC=AD;若以A为圆心,AB为半径作圆,则此圆必过C、D;延长BA交⊙A于E,则BE为⊙A的直径,连接DE,在Rt△BDE中,已知了BE=2a,需求出BD的长;根据DC∥AB,易证得DE=BC=b,则根据勾股定理即可求得BD的长,由此得解.
解答: 解:以A为圆心,以a为半径作圆.延长BA交⊙A于E点,连接ED;(1分)
解:以A为圆心,以a为半径作圆.延长BA交⊙A于E点,连接ED;(1分)
∵AB∥CD,
∴∠CAB=∠DCA,∠DAE=∠CDA;
∵AC=AD,∴∠DCA=∠CDA,
∴∠DAE=∠CAB;(2分)
在△ABC和△DAE中, ;
;
∴△CAB≌△DAE,(3分)
∴ED=BC=b(4分)
∵BE是直径,
∴∠EDB=90°
在Rt△EDB中,
ED=b,BE=2a,
由勾股定理得ED2+BD2=BE2
∴ (5分)
(5分)
∴ .(6分)
.(6分)
点评:此题主要考查了圆周角定理、勾股定理以及全等三角形的判定;能够通过辅助线构建出⊙A是解答本题的关键.
解答:
 解:以A为圆心,以a为半径作圆.延长BA交⊙A于E点,连接ED;(1分)
解:以A为圆心,以a为半径作圆.延长BA交⊙A于E点,连接ED;(1分)∵AB∥CD,
∴∠CAB=∠DCA,∠DAE=∠CDA;
∵AC=AD,∴∠DCA=∠CDA,
∴∠DAE=∠CAB;(2分)
在△ABC和△DAE中,
 ;
;∴△CAB≌△DAE,(3分)
∴ED=BC=b(4分)
∵BE是直径,
∴∠EDB=90°
在Rt△EDB中,
ED=b,BE=2a,
由勾股定理得ED2+BD2=BE2
∴
 (5分)
(5分)∴
 .(6分)
.(6分)点评:此题主要考查了圆周角定理、勾股定理以及全等三角形的判定;能够通过辅助线构建出⊙A是解答本题的关键.

练习册系列答案
 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案
相关题目
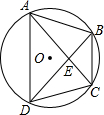 如图,已知四边形ABCD是⊙O的内接四边形,且AB=CD=5,AC=7,BE=3.下列命题错误的是( )
如图,已知四边形ABCD是⊙O的内接四边形,且AB=CD=5,AC=7,BE=3.下列命题错误的是( )| A、△ABE≌△DCE | B、∠BDA=45° | C、S四边形ABCD=24.5 | D、图中全等的三角形共有2对 |
如图,已知四边形ABCD是边长为2的正方形,E是AB的中点,F是BC的中点,AF与DE相交于G,BD和AF相交于H,那么四边形BEGH的面积是( )

A、
| ||
B、
| ||
C、
| ||
D、
|
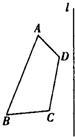 32、如图,已知四边形ABCD和直线L.
32、如图,已知四边形ABCD和直线L.