题目内容
(本题满分10分,其中每小题各5分)
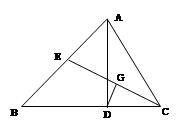
在Rt△ABC中,∠ABC=90°,∠BAC=60°,D为BC中点,连结AD,过点D作DE⊥AD,交AB的延长线于E.

(1)若AD= ,求△ABC的面积;
,求△ABC的面积;
(2)求 的值.
的值.
在Rt△ABC中,∠ABC=90°,∠BAC=60°,D为BC中点,连结AD,过点D作DE⊥AD,交AB的延长线于E.

(1)若AD=
 ,求△ABC的面积;
,求△ABC的面积;(2)求
 的值.
的值.(1)S△ABC=2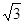 .(2)
.(2) =
=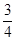 .
.
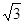 .(2)
.(2) =
=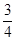 .
.试题分析:解:(1)∵∠ABC=90°,∠BAC=60°,∴∠C=30°,∴AC=2AB (1分)
设AB=k,则AC=2k,BC=
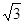 k,∵D为BC中点,∴BD=DC=
k,∵D为BC中点,∴BD=DC=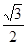 k
k在Rt△ABD中,AB2+BD2=AD2,AD=

∴k2+(
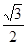 k)2=(
k)2=( )2 (1分)
)2 (1分)∴k=2 (1分)
∴AB=2,BC=2
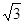 (1分)
(1分)∴
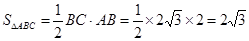 (1分)
(1分)(2)∵AD⊥DE,∴∠ADE=90º,∴∠DAE+∠E=90º
∵∠ABC=90°,∴∠DAE+∠ADB=90°,∴∠ADB=∠E (1分)
∵∠ABD=∠DBE=90°,∴△ABD∽△DBE (1分)
∴
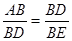 (1分)
(1分)∴
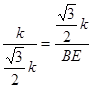 ,∴
,∴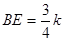 (1分)
(1分)∴
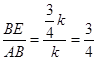 (1分)
(1分)点评:(1)问,应用了直角三角形特殊角与边与边之间的关系,由题意求出边长易得到三角形的面积。(2)中根据已知可证得两个三角形相似,利用相似比,可求出,本题难度不大,属于基础题。

练习册系列答案
相关题目

 绕点
绕点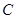 顺利针方向旋转
顺利针方向旋转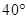 得
得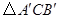 ,若
,若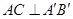 ,则
,则 等于( )
等于( )
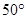 (B)
(B) (C)
(C)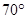 (D)
(D)

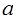 为偶数,且
为偶数,且 ,则这个三角形的周长为_______________。
,则这个三角形的周长为_______________。