题目内容
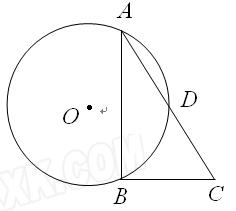
(10分)如图,Rt△ABC中,<ACB=90°,AC="4" ,AB="5" ,点P是AC上的动点(P不与A、C重合),设PC=x,点P到AB的距离PQ为y.
(1)求y与x的函数表达式,并写出自变量x的取值范围;
(2)试讨论以P为圆心、半径长为x的圆与AB所在直线的位置关系,并指出相应的x取值范围.
(1)求y与x的函数表达式,并写出自变量x的取值范围;
(2)试讨论以P为圆心、半径长为x的圆与AB所在直线的位置关系,并指出相应的x取值范围.

解:(1)在Rt△ABC中,由勾股定理可得:BC= .…1分
.…1分
由题意可知:∠PQA=∠C=900,∠A=∠A,AP=AC-PC=4-x,
∴△APQ∽△ABC ∴ ,即:
,即:  , ………………3分
, ………………3分
变形得y与x的函数表达式为: ,
,
其中自变量x的取值范围为:0<x<4. ………………5分
(2)令PC=PQ,即 ,解得:x=
,解得:x= . ………………7分
. ………………7分
∴当 0<x<
0<x< 时,以P为圆心、半径长为x的圆与AB所在直线相离; ………………8分
时,以P为圆心、半径长为x的圆与AB所在直线相离; ………………8分
当x= 时, 以P为圆心、半径长为x的圆与AB所在直线相切; ………………9分
时, 以P为圆心、半径长为x的圆与AB所在直线相切; ………………9分
当 <x<4时,以P为圆心、半径长为x的圆与AB所在直线相交. ………………10分
<x<4时,以P为圆心、半径长为x的圆与AB所在直线相交. ………………10分
 .…1分
.…1分由题意可知:∠PQA=∠C=900,∠A=∠A,AP=AC-PC=4-x,
∴△APQ∽△ABC ∴
 ,即:
,即:  , ………………3分
, ………………3分变形得y与x的函数表达式为:
 ,
,其中自变量x的取值范围为:0<x<4. ………………5分
(2)令PC=PQ,即
 ,解得:x=
,解得:x= . ………………7分
. ………………7分∴当
 0<x<
0<x< 时,以P为圆心、半径长为x的圆与AB所在直线相离; ………………8分
时,以P为圆心、半径长为x的圆与AB所在直线相离; ………………8分当x=
 时, 以P为圆心、半径长为x的圆与AB所在直线相切; ………………9分
时, 以P为圆心、半径长为x的圆与AB所在直线相切; ………………9分当
 <x<4时,以P为圆心、半径长为x的圆与AB所在直线相交. ………………10分
<x<4时,以P为圆心、半径长为x的圆与AB所在直线相交. ………………10分略

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案
相关题目


 中,
中, ,
, ,
, 的圆心为
的圆心为 ,如果图中两个阴影部分的面积相等,那么
,如果图中两个阴影部分的面积相等,那么 的长是 .(结果保留
的长是 .(结果保留 )
)

 为120°,用这个扇形围成一个圆锥的侧面,
为120°,用这个扇形围成一个圆锥的侧面,


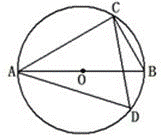
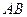 是⊙
是⊙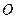 的弦,点D是弧AB的中点,过B作A
的弦,点D是弧AB的中点,过B作A B的垂线交AD的延长线于C.求证:AD=DC.
B的垂线交AD的延长线于C.求证:AD=DC.