题目内容
一个圆锥的底面半径为10cm，母线长为20cm，求：（1）圆锥的高；（2）侧面展开图的圆心角．分析：（1）底面半径为10cm，母线长为20cm，由勾股定理可得圆锥高；
（2）由底面周长与扇形的弧长相等求得圆心角．
（2）由底面周长与扇形的弧长相等求得圆心角．
解答：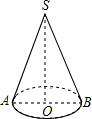
解：（1）如图所示，在Rt△SOA中，
SO=
=
=10
；
（2）设侧面展开图扇形的圆心角度数为n，则由2πr=
，
得n=180，
故侧面展开图扇形的圆心角为180度．
解：（1）如图所示，在Rt△SOA中，SO=
| SA2-OA2 |
| 202-102 |
| 3 |
（2）设侧面展开图扇形的圆心角度数为n，则由2πr=
| nπl |
| 180 |
得n=180，
故侧面展开图扇形的圆心角为180度．
点评：本题利用了勾股定理，弧长公式，圆的周长公式和扇形面积公式求解．
练习册系列答案
相关题目
一个圆锥的底面半径为4cm，高为5cm，则它的表面积是（ ）
| A、12πcm2 | ||
| B、26πcm2 | ||
C、4
| ||
D、（4
|