��Ŀ����
����Ŀ��С�������г����飬�������������̵���һ����Ʒ�ڵ�![]() ����������������Ϣ���±���
����������������Ϣ���±���
ʱ��� |
|
|
�ۼۣ�Ԫ/���� |
| 50 |
ÿ������������ |
| |
��֪����Ʒ�Ľ���Ϊÿ��20Ԫ�������۸���Ʒ��ÿ������Ϊ![]() Ԫ.
Ԫ.
��1�����![]() ��
��![]() �ĺ�����ϵʽ��
�ĺ�����ϵʽ��
��2�������۸���Ʒ�ڼ���ʱ�������������������������Ƕ��٣�
��3������Ʒ�����۹����У����ж�����ÿ������������2400Ԫ����ֱ��д�����.
���𰸡���1��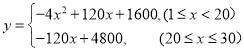 ����2��15��ʱ�������������������������Ϊ2500Ԫ����3��11
����2��15��ʱ�������������������������Ϊ2500Ԫ����3��11
��������
��1����������=ÿ�������������۵ļ�����������ú����Ľ���ʽ��
��2�����ݣ�1���õ�����������ʽ����϶��κ�����һ�κ��������ʿɷֱ�ó����ֵ�������������ıȽϣ��ɵô𰸣�
��3�����ݶ��κ���ֵ���ڻ����2400��һ�κ���ֵ���ڻ����2400���ɵò���ʽ�����ݽⲻ��ʽ���ɵô𰸣�
�⣺(1)��![]() ʱ��
ʱ��
![]() ��
��
��![]() ʱ��
ʱ��
![]() ��
��
���ϣ�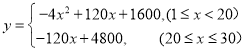
��2����![]() ʱ��
ʱ��
![]()
��![]() ��
��
�൱![]() ʱ��
ʱ��![]() �����ֵ�����ֵΪ2500Ԫ
�����ֵ�����ֵΪ2500Ԫ
��![]() ʱ��
ʱ��
![]() .
.
��![]() ��
��
��![]() ��
��![]() ���������С.
���������С.
�൱![]() ʱ��
ʱ��![]() �����ֵ�����ֵΪ2400Ԫ��
�����ֵ�����ֵΪ2400Ԫ��
���Ͽ�֪����![]() ʱ�������������������������Ϊ2500Ԫ.
ʱ�������������������������Ϊ2500Ԫ.
��3���ٵ�1��x��20ʱ��y=-4x2+120x+1600��2400��
��ã�10��x��20��
���������2400Ԫ��������10��x��20����10�죻
�ڵ�20��x��30ʱ��y=-120x+4800��2400��
��ã�x��20��
���������2400Ԫ��������20��x��20����1�죬
���Ը���Ʒ���������۹����У���11��ÿ������������2400Ԫ��

 ��������ϵ�д�
��������ϵ�д� ��ӡ�Ļ���ʱ����ϵ�д�
��ӡ�Ļ���ʱ����ϵ�д�