题目内容
等腰三角形ABC的一个外角∠DCB=140°,则∠A的度数为
- A.40°
- B.40°或70°
- C.40°或70°或100°
- D.70°或100°
C
分析:由已知等腰△ABC的一个外角∠DCB=140°,可以得出可能底角的外角是140°,也可能顶角的外角是140°,进而得出∠A的度数.
解答:
解:∵等腰△ABC的一个外角∠DCB=140°,
∴①当底角的外角是140°,
∴底角∠A=∠BCA=180°-140°=40°,
②当底角的外角是140°,
∴顶角∠A=180°-2×∠BCA=180°-2×(180°-140°)=100°,
③当顶角的外角是140°,
∴底角∠A=140°÷2=70°.
故∠A的度数为:40°或100°或70°.
故选C.
点评:此题主要考查了等腰三角形的性质,此题应注意进行讨论,容易忽略一种情况.
分析:由已知等腰△ABC的一个外角∠DCB=140°,可以得出可能底角的外角是140°,也可能顶角的外角是140°,进而得出∠A的度数.
解答:

解:∵等腰△ABC的一个外角∠DCB=140°,
∴①当底角的外角是140°,
∴底角∠A=∠BCA=180°-140°=40°,
②当底角的外角是140°,
∴顶角∠A=180°-2×∠BCA=180°-2×(180°-140°)=100°,
③当顶角的外角是140°,
∴底角∠A=140°÷2=70°.
故∠A的度数为:40°或100°或70°.
故选C.
点评:此题主要考查了等腰三角形的性质,此题应注意进行讨论,容易忽略一种情况.

练习册系列答案
相关题目
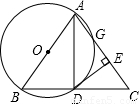
 50、如图,以等腰三角形ABC的一腰AB为直径的⊙O交BC于点D,交AC于点G,连接AD,并过点D作DE⊥AC,垂足为E.根据以上条件写出三个正确结论(除AB=AC,AO=BO,∠ABC=∠ACB外)是:
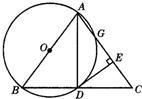
50、如图,以等腰三角形ABC的一腰AB为直径的⊙O交BC于点D,交AC于点G,连接AD,并过点D作DE⊥AC,垂足为E.根据以上条件写出三个正确结论(除AB=AC,AO=BO,∠ABC=∠ACB外)是: 如图,以等腰三角形ABC的一腰AB为直径的⊙O交BC于D,过D作DE⊥AC于E.求证:DE是⊙O的切线.
如图,以等腰三角形ABC的一腰AB为直径的⊙O交BC于D,过D作DE⊥AC于E.求证:DE是⊙O的切线.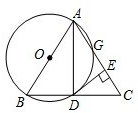 如图,以等腰三角形ABC的一腰AB为直径的⊙O交BC于点D,交AC于点G,连接AD,并过点D作DE⊥AC,垂足为E.根据以上条件写出三个正确结论(除AB=AC,AO=BO,∠ABC=∠ACB外)是:
如图,以等腰三角形ABC的一腰AB为直径的⊙O交BC于点D,交AC于点G,连接AD,并过点D作DE⊥AC,垂足为E.根据以上条件写出三个正确结论(除AB=AC,AO=BO,∠ABC=∠ACB外)是: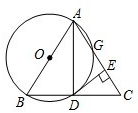 如图,以等腰三角形ABC的一腰AB为直径的⊙O交BC于点D,交AC于点G,连接AD,并过点D作DE⊥AC,垂足为E.根据以上条件写出三个正确结论(除AB=AC,AO=BO,∠ABC=∠ACB外)是:
如图,以等腰三角形ABC的一腰AB为直径的⊙O交BC于点D,交AC于点G,连接AD,并过点D作DE⊥AC,垂足为E.根据以上条件写出三个正确结论(除AB=AC,AO=BO,∠ABC=∠ACB外)是: