题目内容
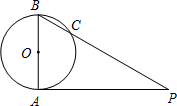如图，已知AB是⊙O的直径，AP是⊙O的切线，A是切点，BP与⊙O交于点C，若AB=2，∠P=30°，求AP的长（结果保留根号）．
解：∵AB是⊙O的直径，AP是⊙O的切线，A是切点，
∴∠PAB=90°，
∵AB=2，∠P=30°，
∴tan30°=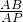
=
=
，
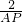∴AP=2
．
分析：利用切线的性质得出∠PAB=90°，进而利用锐角三角函数关系得出AP的长．
点评：此题主要考查了切线的性质和锐角三角函数关系，正确利用锐角三角函数关系是解题关键．
∴∠PAB=90°，
∵AB=2，∠P=30°，
∴tan30°=
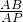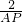==，∴AP=2
．分析：利用切线的性质得出∠PAB=90°，进而利用锐角三角函数关系得出AP的长．
点评：此题主要考查了切线的性质和锐角三角函数关系，正确利用锐角三角函数关系是解题关键．
练习册系列答案
相关题目
如图，已知AB是⊙O的直径，AC是弦，D为AB延长线上一点，DC=AC，∠ACD=120°，BD=10．
如图，已知AB是⊙O的直径，C是⊙O上一点，∠BAC的平分线交⊙O于点D，交⊙O的切线BE于点E，过点D作DF⊥AC，交AC的延长线于点F．
（2013•泰安）如图，已知AB是⊙O的直径，AD切⊙O于点A，点C是
如图，已知AB是⊙O的直径，P为⊙O外一点，且OP∥BC，∠P=∠BAC．
如图，已知AB是圆O的直径，∠DAB的平分线AC交圆O与点C，作CD⊥AD，垂足为点D，直线CD与AB的延长线交于点E．