题目内容
若四边形ABCD的相对的两个内角互补,且满足∠A:∠B:∠C=2:3:4,则∠A=分析:先根据四边形ABCD的相对的两个内角互补,及已知求出∠A,从而得出∠C,∠B,∠D的度数.
解答:解:∵四边形ABCD的相对的两个内角互补,∠A:∠B:∠C=2:3:4,
∴∠A=180°×
=60°,
∴∠C=180°-60°=120°,
∴∠B=
∠A=90°,
∴∠D=180°-90°=90°.
故答案为:60°,90°,120°,90°.
∴∠A=180°×
| 2 |
| 2+4 |
∴∠C=180°-60°=120°,
∴∠B=
| 3 |
| 2 |
∴∠D=180°-90°=90°.
故答案为:60°,90°,120°,90°.
点评:本题考查多边形的内角,解题关键是根据补角的定义及比例式找到相互间的关系.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,在正方形ABCD中,E是BC边上的一点,以E为圆心,EC为半径的半圆与以A为圆心,AB为半径的圆弧相外切F,若AB=4,
如图,在正方形ABCD中,E是BC边上的一点,以E为圆心,EC为半径的半圆与以A为圆心,AB为半径的圆弧相外切F,若AB=4, 如图,在平行四边形ABCD中,AB=5,BC=10,F为AD的中点,CE⊥AB于E,设∠ABC=α(60°≤α<90°).
如图,在平行四边形ABCD中,AB=5,BC=10,F为AD的中点,CE⊥AB于E,设∠ABC=α(60°≤α<90°).
 ,AD=3,BE=2,求BF的长.
,AD=3,BE=2,求BF的长.
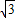 ,AD=3,BE=2,求BF的长.
,AD=3,BE=2,求BF的长.