题目内容
【题目】在![]() 中,
中,![]() ,
,![]() ,将
,将![]() 绕点
绕点![]() 顺时针旋转角
顺时针旋转角![]() 得
得![]() ,
,![]() 交
交![]() 于点
于点![]() ,
,![]() 分别交
分别交![]() 、
、![]() 于
于![]() 、
、![]() 两点.
两点.
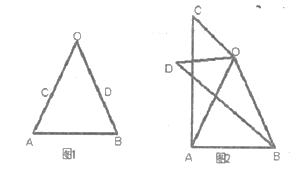
![]() 如图
如图![]() ,观察并猜想:图中在不连接其它线段的情况下,共有多少对全等三角形(不包含
,观察并猜想:图中在不连接其它线段的情况下,共有多少对全等三角形(不包含![]() )?将它们全部写出来,并且选一组全等三角形进行证明;
)?将它们全部写出来,并且选一组全等三角形进行证明;
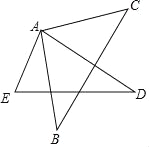
![]() 如图
如图![]() ,当
,当![]() 时,求
时,求![]() 的长.
的长.

【答案】(1)详见解析;(2)![]() .
.
【解析】
(1)因为AB=BC,由旋转的性质可知,∠A=∠C=∠C1,AB=BC=BC1,∠ABE=∠C1BF,可证△ABE≌△C1BF;由△ABE≌△C1BF得BE=BF,故AE=ABBE=BCBF=CF,∠A1=∠C,可证△DAE≌△DCF;由△DAE≌△DCF得DE=DF,及BE=BF,BD=BD,可证△DEB≌△DFB;由A1B=BC,A1D=DC,BD=BD,可证△ABD≌△C1BD;同理可证△A1BD≌△CBD.
(2)当a=30°时,在△ABE中,∠A=∠EBA=30°,AB=2,作EG⊥AB,垂足为G,解直角三角形求BE.
共![]() 组:
组:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ;
;
证明:∵AB=BC,
∴∠A=∠C,
由旋转可知,AB=BC1,∠A=∠C1,∠ABE=∠C1BF,
∴△ABE≌△C1BF;
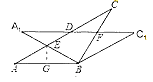
![]() 当
当![]() 时,如图,作
时,如图,作![]() ,垂足为
,垂足为![]() ,
,
∵在![]() 中,
中,![]() ,
,![]() ,
,
∴![]() ,
,
在![]() 中,
中,![]() ,
,
∴![]() .
.

练习册系列答案
相关题目