Question

【题目】正方形ABCD的边长是4，点P是AD边的中点，点E是正方形边上的一点．若△PBE是等腰三角形，则腰长为 ．

Answer 1

【答案】2 ，或 ，或
【解析】解：分情况讨论：（1）当PB为腰时，若P为顶点，则E点与C点重合，如图所示：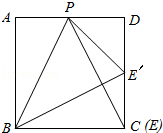
∵四边形ABCD是正方形，
∴AB=BC=CD=AD=4，∠A=∠C=∠D=90°，
∵P是AD的中点，
∴AP=DP=2，
根据勾股定理得：BP= = =2 ；
若B为顶点，则根据PB=BE′得，E′为CD中点，此时腰长PB=2 ；（2）当PB为底边时，E在BP的垂直平分线上，与正方形的边交于两点，即为点E；①当E在AB上时，如图2所示：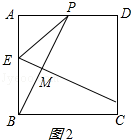

则BM= BP= ，
∵∠BME=∠A=90°，∠MBE=∠ABP，
∴△BME∽△BAP，
∴ ，即 ，
∴BE= ；②当E在CD上时，如图3所示：

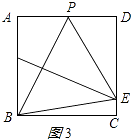
设CE=x，则DE=4﹣x，
根据勾股定理得：BE2=BC2+CE2 ， PE2=DP2+DE2 ，
∴42+x2=22+（4﹣x）2 ，
解得：x= ，
∴CE= ，
∴BE= = = ；
综上所述：腰长为：2 ，或 ，或 ；
故答案为：2 ，或 ，或 ．
分情况讨论：（1）当PB为腰时，若P为顶点，则E点和C点重合，求出PB长度即可；若B为顶点，则E点为CD中点；（2）当PB为底时，E在BP的垂直平分线上，与正方形的边交于两点，即为点E；①由题意得出BM= BP= ，证明△BME∽△BAP，得出比例式 ，即可求出BE；②设CE=x，则DE=4﹣x，根据勾股定理得出方程求出CE，再由勾股定理求出BE即可．