题目内容
【题目】已知△ABC的外角∠CBE,∠BCF的角平分线BP,CP交于P点,则∠BPC是( )
A.钝角
B.锐角
C.直角
D.无法确定
【答案】B
【解析】解: 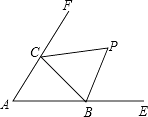
∵△ABC的外角平分线BP,CP交于P点,
∴∠PBC= ![]() ∠EBC,∠BCP=
∠EBC,∠BCP= ![]() ∠BCF,
∠BCF,
∵∠CBE、∠BCF是△ABC的两个外角,
∴∠CBE+∠BCF=360°﹣(180°﹣∠A)=180°+∠A,
∴∠PBC+∠BCP= ![]() (∠EBC+∠BCF)=
(∠EBC+∠BCF)= ![]() (180°+∠A)=90°+
(180°+∠A)=90°+ ![]() ∠A,
∠A,
∵在△PBC中,∠BPC=180°﹣(∠PBC+∠BCP)=180°﹣(90°+ ![]() ∠A)=90°﹣
∠A)=90°﹣ ![]() ∠A<90°,
∠A<90°,
∴∠BPC是锐角.
故选:B.
首先根据△ABC的外角平分线BP,CP交于P点,得出∠PBC+∠BCP=90°+ ![]() ∠A,再根据三角形内角和定理,求得∠BPC=90°﹣
∠A,再根据三角形内角和定理,求得∠BPC=90°﹣ ![]() ∠A<90°即可.
∠A<90°即可.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目