题目内容
【题目】如图①,在平面直角坐标系中,直径为![]() 的⊙A经过坐标系原点O(0,0),与x轴交于点B,与y轴交于点C(0,
的⊙A经过坐标系原点O(0,0),与x轴交于点B,与y轴交于点C(0,![]() ).
).
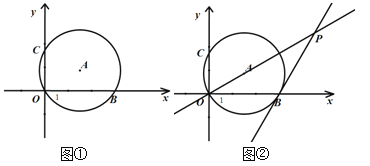
(1)求点B的坐标;
(2)如图②,过点B作⊙A的切线交直线OA于点P,求点P的坐标;
(3)过点P作⊙A的另一条切线PE,请直接写出切点E的坐标.
【答案】(1)![]() (2)
(2)![]() .(3)
.(3)![]()
【解析】
试题分析:(1)、连接![]() .利用圆周角定理和勾股定理求出线段OB的长即可得出点B的坐标;(2)、过点
.利用圆周角定理和勾股定理求出线段OB的长即可得出点B的坐标;(2)、过点![]() 作
作![]() 轴于点
轴于点![]() .先根据条件求出
.先根据条件求出![]() ,然后得出BP的长,再解Rt
,然后得出BP的长,再解Rt![]() 得出BD、PD的长,然后可得点P的坐标;(3)、类比(2)的做法可得出点E的坐标.
得出BD、PD的长,然后可得点P的坐标;(3)、类比(2)的做法可得出点E的坐标.
试题解析:(1)、如图①,连接![]() .
.

∵![]() , ∴
, ∴![]() 是⊙
是⊙![]() 的直径. ∴
的直径. ∴![]() , ∵
, ∵![]() , ∴
, ∴![]() .
.
∴![]() . ∴
. ∴![]() .
.
(2)、如图②,过点![]() 作
作![]() 轴于点
轴于点![]() .
.

∵![]() 为⊙
为⊙![]() 的切线, ∴
的切线, ∴![]() . 在Rt中,
. 在Rt中,![]() ,
,![]() ,
,
∴![]() . ∴
. ∴![]() . ∴
. ∴![]() .
.
∴![]() . ∴
. ∴![]() .
.
在Rt![]() 中,
中,![]() ,
,![]() ,
,![]() , ∴
, ∴![]() ,
,![]() .
.
∵![]() , ∴
, ∴![]() . ∴
. ∴![]() .
.
(3)![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

