题目内容
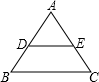
 如图,已知等边△ABC,AC=AD,且AC⊥AD,垂足为点A,则∠BEC的度数为________.
如图,已知等边△ABC,AC=AD,且AC⊥AD,垂足为点A,则∠BEC的度数为________.
75°
分析:由等边△ABC,AC⊥AD,可求得∠BAC与∠BAD的度数,又由AC=AD,即可求得∠ABD的度数,然后由三角形外角的性质,求得∠BEC的度数.
解答:∵△ABC是等边三角形,
∴∠BAC=60°,
∵AC⊥AD,
∴∠CAD=90°,
∴∠BAD=∠BAC+∠CAD=150°,
∵AB=AD,
∴∠ABD=∠D= =15°,
=15°,
∴∠BEC=∠ABD+∠BAC=15°+60°=75°.
故答案为:75°.
点评:此题考查了等边三角形的性质、等腰三角形的性质、垂直的定义以及三角形外角的性质.此题难度不大,注意掌握数形结合思想的应用.
分析:由等边△ABC,AC⊥AD,可求得∠BAC与∠BAD的度数,又由AC=AD,即可求得∠ABD的度数,然后由三角形外角的性质,求得∠BEC的度数.
解答:∵△ABC是等边三角形,
∴∠BAC=60°,
∵AC⊥AD,
∴∠CAD=90°,
∴∠BAD=∠BAC+∠CAD=150°,
∵AB=AD,
∴∠ABD=∠D=
 =15°,
=15°,∴∠BEC=∠ABD+∠BAC=15°+60°=75°.
故答案为:75°.
点评:此题考查了等边三角形的性质、等腰三角形的性质、垂直的定义以及三角形外角的性质.此题难度不大,注意掌握数形结合思想的应用.

练习册系列答案
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案
相关题目
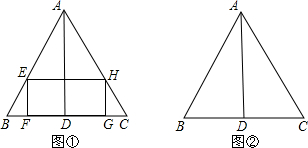
 (2013•黄浦区二模)如图,已知等边△ABC的边长为1,设
(2013•黄浦区二模)如图,已知等边△ABC的边长为1,设
 如图,已知等边三角形ABC的边长为10,点P、Q分别为边AB、AC上的一个动点,点P从点B出发以1cm/s的速度向点A运动,点Q从点C出发以2cm/s的速度向点A运动,连接PQ,以Q为旋转中心,将线段PQ按逆时针方向旋转60°得线段QD,若点P、Q同时出发,则当运动
如图,已知等边三角形ABC的边长为10,点P、Q分别为边AB、AC上的一个动点,点P从点B出发以1cm/s的速度向点A运动,点Q从点C出发以2cm/s的速度向点A运动,连接PQ,以Q为旋转中心,将线段PQ按逆时针方向旋转60°得线段QD,若点P、Q同时出发,则当运动