Question

如图：已知E、F分别是□ABCD的边BC、AD上的点，且BE=DF．

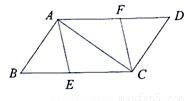
（1）求证：四边形AECF是平行四边形；

（2）若BC＝10，∠BAC＝90°，且四边形AECF是菱形，求BE的长 ．

 

Answer 1

【答案】

（1）证明见解析；（2）5.

【解析】

试题分析：（1）首先由已知证明AF∥EC，BE=DF，推出四边形AECF是平行四边形.（2）由已知先证明AE=BE，即BE=AE=CE，从而求出BE的长.

试题解析：（1）∵四边形ABCD是平行四边形，∴AD∥BC，AD＝BC. ∴AF∥EC.

∵BE＝DF，∴AF＝EC. ∴四边形AECF是平行四边形.

（2）如图，∵四边形AECF是菱形，∴AE＝EC。∴∠1＝∠2.

∵∠3＝90°－∠2，∠4＝90°－∠1，∴∠3＝∠4.

∴AE＝BE.

∴BE＝AE＝CE＝BC＝5.

考点：1.平行四边形的判定和性质；2.菱形的性质；3.等腰三角形的性质；4.三角形内角和定理.