题目内容
一正三角形ABC,A(0,0),B(-4,0),C(-2,3
),将三角形ABC绕原点顺时针旋转120°得到的三角形的三个顶点坐标分别是
| 2 |
(0,0),(2,2
),(4,0)
| 3 |
(0,0),(2,2
),(4,0)
.| 3 |
分析:可以根据旋转的选择求解,旋转不改变图形的大小和形状.
解答:解:把正△ABC的绕原点按顺时针方向旋转120°,就是把它上面的各个点按顺时针方向旋转120度.点A是原点,所以坐标不变,点B在x轴负半轴上,且OB=4,旋转到第一象限,则旋转后B′点的坐标是(2,2
);
OC=4,点C正好旋转到x轴的正半轴上,故点C′坐标为(4,0),
三角形的三个顶点坐标分别是:(0,0),(2,2
),(4,0).
故答案为:(0,0),(2,2
),(4,0).
| 3 |
OC=4,点C正好旋转到x轴的正半轴上,故点C′坐标为(4,0),
三角形的三个顶点坐标分别是:(0,0),(2,2
| 3 |
故答案为:(0,0),(2,2
| 3 |
点评:此题主要考查了图形的旋转,是一道考查数与形结合的好试题,也为高中后续学习做了良好的铺垫.从考试情况看,还有非常多考生没完全理解旋转的三大要素即中心、方向、角度,故失分的较多.

练习册系列答案
相关题目
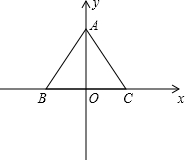 如图,坐标平面中有一正三角形ABC,边长为2,
如图,坐标平面中有一正三角形ABC,边长为2,