题目内容
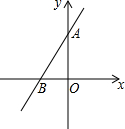如图，已知直线y=| 4 | 3 |
（1）求点A关于x轴对称点A′的坐标；
（2）求线段AB的长．
分析：（1）把y=0代入函数解析式可求x=-3，从而可得B点坐标；同理可求A点坐标；
（2）由于△AOB是直角三角形，利用勾股定理易求AB．
（2）由于△AOB是直角三角形，利用勾股定理易求AB．
解答：解：（1）如图，
当y=0时，x=-3，
当x=0时，y=4，
故A点坐标是（0，4），B点坐标是（-3，0），
∴点A关于x轴对称点A′的坐标是（0，-4）；
（2）在Rt△AOB中，AB=
=
=5．
当y=0时，x=-3，
当x=0时，y=4，
故A点坐标是（0，4），B点坐标是（-3，0），
∴点A关于x轴对称点A′的坐标是（0，-4）；
（2）在Rt△AOB中，AB=
| OA2+OB2 |
| 32+42 |
点评：本题考查了一次函数综合题、勾股定理．解题的关键是熟练掌握勾股定理．
练习册系列答案
优等生题库系列答案
53天天练系列答案
相关题目
16、如图，已知直线AB和CD相交于点O，∠COE是直角，OF平分∠AOE．
5、如图，已知直线l1∥l2，AB⊥CD，∠1=30°，则∠2的度数为（ ）
如图，已知直线l1：
（2013•怀化）如图，已知直线a∥b，∠1=35°，则∠2=
如图，已知直线m∥n，则下列结论成立的是（ ）