题目内容
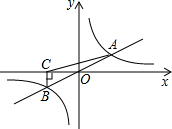 (2011•黔东南州)如图所示,反比例函数y=
(2011•黔东南州)如图所示,反比例函数y=| k |
| x |
y=
| 3 |
| x |
y=
.| 3 |
| x |
分析:根据反比例函数y=
的图象关于原点对称,可求出A、B两点坐标的关系,设出两点坐标再根据三角形的面积公式即可解答.
| k |
| x |
解答:解:∵反比例函数y=
的图象关于原点对称,
∴设A点坐标为(x,
),则B点坐标为(-x,-
),
∴S△BOC=
OC•BC=
x•
=
,
S△AOC=
OC•|-
|=
|-x|•|-
|=
,
∴S△ABC=S△COB+S△AOC=k=3.
∴这个反比例函数的解析式为:y=
.
故答案为:y=
.
| k |
| x |
∴设A点坐标为(x,
| k |
| x |
| k |
| x |
∴S△BOC=
| 1 |
| 2 |
| 1 |
| 2 |
| k |
| x |
| k |
| 2 |
S△AOC=
| 1 |
| 2 |
| 1 |
| x |
| 1 |
| 2 |
| k |
| x |
| k |
| 2 |
∴S△ABC=S△COB+S△AOC=k=3.
∴这个反比例函数的解析式为:y=
| 3 |
| x |
故答案为:y=
| 3 |
| x |
点评:本题考查的是反比例函数与正比例函数图象的特点,解答此题的关键是找出A、B两点坐标的关系,设出两点坐标即可.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
 (2011•黔东南州)用若干个大小相同、棱长为1的小正方体搭成一个几何体模型,其三视图如图所示,则搭成这个几何体模型所用的小正方体的个数是( )
(2011•黔东南州)用若干个大小相同、棱长为1的小正方体搭成一个几何体模型,其三视图如图所示,则搭成这个几何体模型所用的小正方体的个数是( )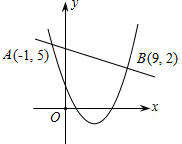 (2011•黔东南州)如图,一次函数y1=kx+n(k≠0)与二次函数y2=ax2+bx+c(a≠0)的图象相交于A(-1,5)、B(9,2)两点,则关于x的不等式kx+n≥ax2+bx+c的解集为( )
(2011•黔东南州)如图,一次函数y1=kx+n(k≠0)与二次函数y2=ax2+bx+c(a≠0)的图象相交于A(-1,5)、B(9,2)两点,则关于x的不等式kx+n≥ax2+bx+c的解集为( )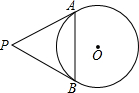 (2011•黔东南州)如图,PA、PB是⊙O的切线,切点分别为A、B,已知⊙O的半径为2,∠P=60°,则弦AB的长为
(2011•黔东南州)如图,PA、PB是⊙O的切线,切点分别为A、B,已知⊙O的半径为2,∠P=60°,则弦AB的长为