题目内容
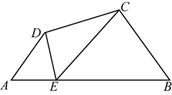
在四边形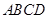 中,
中,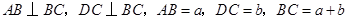 ,且
,且 .取
.取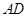 的中点
的中点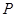 ,连结
,连结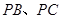 .
.

(1)试判断三角形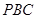 的形状;
的形状;
(2)在线段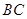 上,是否存在点
上,是否存在点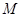 ,使
,使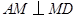 .若存在,请求出
.若存在,请求出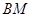 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.
【答案】
(1)等腰直角三角形(2)存在,当 时,有一点
时,有一点 ,
, ;当
;当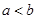 时,有两点
时,有两点 ,
,
【解析】解:(1)在四边形 中,
中,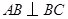 ,
, ,
,
 四边形
四边形 为直角梯形(或矩形).
为直角梯形(或矩形).
过点 作
作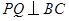 ,垂足为
,垂足为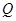 ,
, ,
,

又点 是
是 的中点,
的中点, 点
点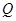 是
是 的中点,
的中点,
又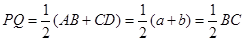 ,
,
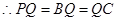 ,
,
 与
与 是全等的等腰直角三角形,
是全等的等腰直角三角形,
 ,
,
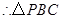 是等腰直角三角形.
是等腰直角三角形.
(2)存在点 使
使 .
.
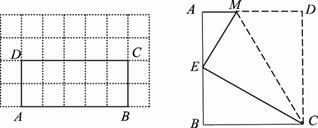
以 为直径,
为直径, 为圆心作圆
为圆心作圆 .
.
当 时,四边形
时,四边形 为矩形,
为矩形, ,
,
圆 与
与 相切于点
相切于点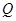 ,此时,
,此时, 点与
点与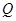 点重合,存在点
点重合,存在点 ,使得
,使得 ,
,
此时 .
.
当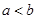 时,四边形
时,四边形 为直角梯形,
为直角梯形,
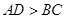 ,
, ,圆心
,圆心 到
到 的距离
的距离 小于圆
小于圆 的半径,圆
的半径,圆 与
与 相交,
相交, 上存在两点
上存在两点 ,使
,使 ,
,
过点 作
作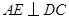 ,在
,在 中,
中, ,
,
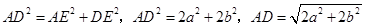
连结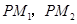 ,则
,则 ,
,
在直角三角形 中,
中, ,
,
 .
.
同理可得: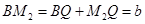 .
.
综上所述,在线段 上存在点
上存在点 ,使
,使 .
.
当 时,有一点
时,有一点 ,
, ;当
;当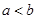 时,有两点
时,有两点 ,
, .
.
根据已知条件,得到四边形ABCD为直角梯形或矩形.
(1)过点P作PQ⊥BC,易证PQ=BQ=QC,则△PQB与△PQC是全等的等腰直角三角形,因而△PBC是等腰直角三角形.
(2)判断在线段BC上,是否存在点M,使AM⊥MD,利用相似三角形的性质与判定得出即可.

练习册系列答案
相关题目

 中,
中,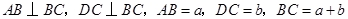 ,且
,且 .取
.取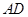 的中点
的中点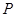 ,连结
,连结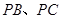 .
.
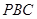 的形状;
的形状;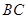 上,是否存在点
上,是否存在点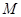 ,使
,使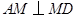 .若存在,请求出
.若存在,请求出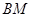 的长;若不存在,请说明理由.
的长;若不存在,请说明理由. 的值.
的值.