题目内容
 如图,在直角梯形中,底AB=13,CD=8,AD⊥AB,并且AD=12,则A到BC的距离为________.
如图,在直角梯形中,底AB=13,CD=8,AD⊥AB,并且AD=12,则A到BC的距离为________.
12
分析:本题可以通过作辅助线解决,过C作CF⊥AB于F,过A作AE⊥BC于E.由梯形和直角三角形的性质易求得BC=AB=13,再根据条件可判定△ABE≌△CBF,即可得AE=CF,即可得解.
解答: 解:如图,过C作CF⊥AB于F,过A作AE⊥BC于E,
解:如图,过C作CF⊥AB于F,过A作AE⊥BC于E,
∵在直角梯形中,AD⊥AB,CF⊥AB,
∴DC=AF=8,AD=FC=12,FB=AB-AF=13-8=5,
在直角三角形CFB中,根据勾股定理得:BC= =
= =13;
=13;
∴BC=AB;
又∵CF⊥AB,AE⊥BC,且∠B为公共角,
∴△ABE≌△CBF(AAS);
∴AE=CF=12,
AE即为所求A到BC的距离.
故答案为:12.
点评:本题考查了直角梯形的性质、勾股定理的应用、全等三角形的判定和性质,是一道难度中等的综合题,解题的关键是正确作出辅助线.
分析:本题可以通过作辅助线解决,过C作CF⊥AB于F,过A作AE⊥BC于E.由梯形和直角三角形的性质易求得BC=AB=13,再根据条件可判定△ABE≌△CBF,即可得AE=CF,即可得解.
解答:
 解:如图,过C作CF⊥AB于F,过A作AE⊥BC于E,
解:如图,过C作CF⊥AB于F,过A作AE⊥BC于E,∵在直角梯形中,AD⊥AB,CF⊥AB,
∴DC=AF=8,AD=FC=12,FB=AB-AF=13-8=5,
在直角三角形CFB中,根据勾股定理得:BC=
 =
= =13;
=13;∴BC=AB;
又∵CF⊥AB,AE⊥BC,且∠B为公共角,
∴△ABE≌△CBF(AAS);
∴AE=CF=12,
AE即为所求A到BC的距离.
故答案为:12.
点评:本题考查了直角梯形的性质、勾股定理的应用、全等三角形的判定和性质,是一道难度中等的综合题,解题的关键是正确作出辅助线.

练习册系列答案
相关题目
 20、如图,在直角梯形中,底AD=6 cm,BC=11 cm,腰CD=12 cm,则这个直角梯形的周长为
20、如图,在直角梯形中,底AD=6 cm,BC=11 cm,腰CD=12 cm,则这个直角梯形的周长为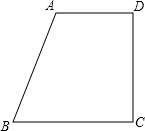 如图,在直角梯形中,AD=6cm,BC=11cm,CD=12cm,则AB的长为
如图,在直角梯形中,AD=6cm,BC=11cm,CD=12cm,则AB的长为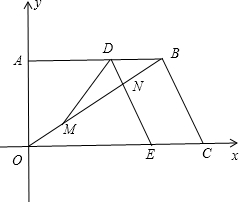 DE由CB出发沿BA方向匀速运动,速度为1单位/秒,交OB于点N,连接DM.若没运动时间为t(s)(0<t<8).
DE由CB出发沿BA方向匀速运动,速度为1单位/秒,交OB于点N,连接DM.若没运动时间为t(s)(0<t<8). 如图,在直角梯形中,上底AC=6cm,下底BD=11cm,CD⊥BD且腰CD=12cm,则这个直角梯形的周长为
如图,在直角梯形中,上底AC=6cm,下底BD=11cm,CD⊥BD且腰CD=12cm,则这个直角梯形的周长为 中,
中,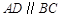 ,
, ,
, ,
, .
. 边上一点,过点
边上一点,过点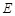 作EF⊥DC于点F.求证
作EF⊥DC于点F.求证 .
.