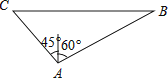��Ŀ����
����Ŀ����֪��������x�ύ��A��6��0����B���� ![]() ��0�����㣬��y�ύ�ڵ�C�����������ϵ�M��1��3����MN��x���ڵ�N������OM��
��0�����㣬��y�ύ�ڵ�C�����������ϵ�M��1��3����MN��x���ڵ�N������OM�� 
��1����������ߵĽ���ʽ��
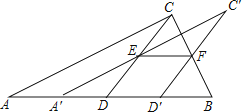
��2����ͼ1������OMN��x������ƽ��t����λ��0��t��5������O��M��N���λ�ã�MN�䡢M��O����ֱ��AC�ֱ��ڵ�E��F��
�ٵ���FΪM��O����е�ʱ����t��ֵ��
����ͼ2����ֱ��M��N�����������ཻ�ڵ�G������G��GH��M��O�佻AC�ڵ�H����ȷ���߶�EH�Ƿ�������ֵ�������ڣ�����������ֵ����ʱt��ֵ���������ڣ���˵�����ɣ�
���𰸡�
��1��
�⣺�������߽���ʽΪy=a��x��6����x+ ![]() �����ѵ�M��1��3�������a=��
�����ѵ�M��1��3�������a=�� ![]() ��
��
�������߽���ʽΪy=�� ![]() ��x��6����x+
��x��6����x+ ![]() ����
����
��y=�� ![]() x2+
x2+ ![]() x+2��
x+2��
��2��
�⣺����ͼ1�У�AC��OM���ڵ�G������EO�䣮
��AO=6��OC=2��MN=3��ON=1��
�� ![]() =3��
=3��
�� ![]() ���ߡ�AOC=��MON=90�㣬
���ߡ�AOC=��MON=90�㣬
���AOC�ס�MNO��
���OAC=��NMO��
�ߡ�NMO+��MON=90�㣬
���MON+��OAC=90�㣬
���AGO=90�㣬
��OM��AC��
�ߡ�M��N��O�����ɡ�MNOƽ�����ã�
��O��M���OM��
��O��M���AC��
��M��F=FO�䣬
��EM��=EO�䣬
��EN���CO��
�� ![]() ��
��
�� ![]() ��
��
��EN��= ![]() ��5��t����
��5��t����
��RT��EO��M������O��N��=1��EN��= ![]() ��5��t����EO��=EM��=
��5��t����EO��=EM��= ![]() +
+ ![]() t��
t��
�ࣨ ![]() +
+ ![]() t��2=1+��
t��2=1+�� ![]() ��
�� ![]() t��2��
t��2��
��t=1��
����ͼ2�У�

��GH��O��M�䣬O��M���AC��
��GH��AC��
���GHE=90�㣬
�ߡ�EGH+��HEG=90�㣬��AEN��+��OAC=90�㣬��HEG=��AEN�䣬
���OAC=��HGE���ߡ�GHE=��AOC=90�㣬
���GHE�ס�AOC��
�� ![]() =
= ![]() ��
��
��EG���ʱ��EH���
��EG=GN�䩁EN��=�� ![]() ��t+1��2+
��t+1��2+ ![]() ��t+1��+2��
��t+1��+2�� ![]() ��5��t��=��
��5��t��=�� ![]() t2+
t2+ ![]() t+
t+ ![]() =��
=�� ![]() ��t��2��2+
��t��2��2+ ![]() ��
��
��t=2ʱ��EG���ֵ= ![]() ��
��
��EH���ֵ= ![]() ��
��
��t=2ʱ��EH���ֵΪ ![]() ��
��
����������1���������߽���ʽΪy=a��x��6����x+ ![]() �����ѵ�M��1��3�����뼴�����a������������⣮
�����ѵ�M��1��3�����뼴�����a������������⣮
��2������ͼ1�У�AC��OM���ڵ�G������EO�䣬����֤����AOC�ס�MNO���Ƴ�OM��AC����RT��EO��M���У����ù��ɶ����г����̼��ɽ�����⣮ ���ɡ�GHE�ס�AOC�� ![]() =
= ![]() =
= ![]() ������EG���ʱ��EH��������κ������EG�����ֵ���ɽ�����⣮���⿼����κ����ۺ��⡢���������ε��ж������ʡ����ɶ�����֪ʶ������Ĺؼ��Ƿ���OM��CA��ѧ������ת����˼�������⣬ѧ�ṹ�����κ��������ֵ���⣬�����п�ѹ���⣮
������EG���ʱ��EH��������κ������EG�����ֵ���ɽ�����⣮���⿼����κ����ۺ��⡢���������ε��ж������ʡ����ɶ�����֪ʶ������Ĺؼ��Ƿ���OM��CA��ѧ������ת����˼�������⣬ѧ�ṹ�����κ��������ֵ���⣬�����п�ѹ���⣮
�����㾫����������Ŀ����֪������������������������Ľ�������֪ʶ���Եõ�����Ĵ𰸣���Ҫ����һԪ���η��̵Ľ������Ӧ�Ķ��κ�����ͼ����x��Ľ������꣮���һԪ���η����е�b2-4ac���ڶ��κ����б�ʾͼ����x���Ƿ��н��㣮��b2-4ac>0ʱ��ͼ����x�����������㣻��b2-4ac=0ʱ��ͼ����x����һ�����㣻��b2-4ac<0ʱ��ͼ����x��û�н��㣮

 ��У����ϵ�д�
��У����ϵ�д�