题目内容
如图在平行四边形ABCD中，点E在AD边上，AE=
DE，连接AC与BE交于点P，若点Q为CD的中点，则S△APE：S四边形PQDE________．
2：13
分析：根据相似三角形的性质，先证△APE∽△CPB，再求其相似比，进而求出S△APE：S四边形PQDE的值．
解答：
解：由题意可得，△APE∽△CPB
则AP：PC=AE：BC=1：3
连接PD，
则S△APD=
S△ACD=
S?ABCD，S△PCD=
S△ACD=
S?ABCD
又AE=DE，Q为CD的中点
则S△APE=
S△APD=
S?ABCD，S△PED=23
S△APD=
S?ABCD，S△PDQ=S△PCD=
S?ABCD，
则S四边形PQDE=S△PED+S△PDQ=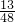
S?ABCD
则S△APE：S四边形PQDE=S?ABCD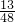：S?ABCD=2：13．
点评：本题主要考查了相似三角形的性质，相似三角形面积的比等于相似比的平方．
分析：根据相似三角形的性质，先证△APE∽△CPB，再求其相似比，进而求出S△APE：S四边形PQDE的值．
解答：
解：由题意可得，△APE∽△CPB则AP：PC=AE：BC=1：3
连接PD，
则S△APD=
S△ACD=S?ABCD，S△PCD=S△ACD=S?ABCD又AE=
DE，Q为CD的中点则S△APE=
S△APD=S?ABCD，S△PED=23S△APD=S?ABCD，S△PDQ=S△PCD=S?ABCD，则S四边形PQDE=S△PED+S△PDQ=
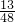S?ABCD则S△APE：S四边形PQDE=
S?ABCD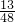：S?ABCD=2：13．点评：本题主要考查了相似三角形的性质，相似三角形面积的比等于相似比的平方．
练习册系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
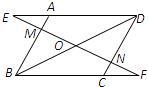21、已知：如图在平行四边形ABCD中，过对角线BD的中点O作直线EF分别交DA的延长线、AB、DC、BC的延长线于点E、M、N、F．
7、如图在平行四边形ABCD中，如果AB=5，AD=9，∠ABC的平分线交AD于点E，交CD的延长线于点F，则DF=
已知如图在平行四边形ABCD中，E、F分别为边AB、CD的中点，BD是对角线．
如图在平行四边形ABCD中，AD=4cm，AB=2cm，则平行四边形ABCD的周长等于（ ）