题目内容
【题目】把(sinα)2记作sin2α,根据图1和图2完成下列各题.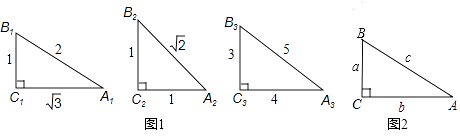
(1)sin2A1+cos2A1= , sin2A2+cos2A2= , sin2A3+cos2A3=;
(2)观察上述等式猜想:在Rt△ABC中,∠C=90°,总有sin2A+cos2A=;
(3)如图2,在Rt△ABC中证明(2)题中的猜想:
(4)已知在△ABC中,∠A+∠B=90°,且sinA= ![]() ,求cosA.
,求cosA.
【答案】
(1)1,1,1
(2)1
(3)在图2中,∵sinA= ![]() ,cosA=
,cosA= ![]() ,且a2+b2=c2,
,且a2+b2=c2,
则sin2A+cos2A=( ![]() )2+(
)2+( ![]() )2=
)2= ![]() +
+ ![]() =
= ![]() =
= ![]() =1,
=1,
即sin2A+cos2A=1;
(4)在△ABC中,∠A+∠B=90°,
∴∠C=90°,
∵sin2A+cos2A=1,
∴( ![]() )2+cosA2=1,
)2+cosA2=1,
解得:cosA= ![]() 或cosA=﹣
或cosA=﹣ ![]() (舍),
(舍),
∴cosA= ![]() .
.
【解析】解:(1)sin2A1+cos2A1=( ![]() )2+(
)2+( ![]() )2=
)2= ![]() +
+ ![]() =1,
=1,
sin2A2+cos2A2=( ![]() )2+(
)2+( ![]() )2=
)2= ![]() +
+ ![]() =1,
=1,
sin2A3+cos2A3=( ![]() )2+(
)2+( ![]() )2=
)2= ![]() +
+ ![]() =1,
=1,
所以答案是:1、1、1;(2)观察上述等式猜想:在Rt△ABC中,∠C=90°,总有sin2A+cos2A=1,
所以答案是:1.
【考点精析】解答此题的关键在于理解解直角三角形的相关知识,掌握解直角三角形的依据:①边的关系a2+b2=c2;②角的关系:A+B=90°;③边角关系:三角函数的定义.(注意:尽量避免使用中间数据和除法).

练习册系列答案
相关题目