Question

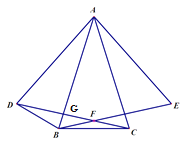
【题目】如图，已知△ABC中，AB＝AC，分别在AB的右侧、AC的左侧作等边△ABE和等边△ACD，BE与CD相交于点F，连接BD，若BD=BF,则∠BDF为__________度.

Answer 1

【答案】20

【解析】

设∠BDF=α，由BD=BF可得∠BFD=α，则∠ADB=∠ABD=60°+α，利用三角形的内角和是180°即可求出∠BAD，利用三角形外角的性质可得∠AGC=60°+α，而∠ACD=60°，在△AGC中利用三角形的内角和是180°可得∠GAC，然后根据∠BAD+∠GAC=60°列出方程即可求出α的值．

解：设∠BDF=α，

∵BD=BF，

∴∠BFD=∠BDF=α．

∵AB=AC，△ACD和△ABE都是等边三角形，

∴AD=AB，∠ADC=∠ABE=∠ACD=∠DAC=60°，

∴∠ADB=∠ABD=60°+α，

在△ADB中，

∠BAD=180°-∠ADB-∠ABD=180°-(60°+α)-(60°+α)=60°-2α．

∵∠AGC是△BGF的外角，

∴∠AGC=∠ABE+∠BFD=60°+α，

在△AGC中

∠GAC=180°-∠AGC-∠ACD=180°-(60°+α)-60°=60°-α，

又∠BAD+∠GAC=∠DAC，

∴60°-2α+60°-α=60°，

解得：α=20°．

故答案为：20．