Question

【题目】如图，∠MON=90°，点A，B分别在射线OM，ON上运动，BE平分∠NBA，BE的反向延长线与∠BAO的平分线交于点C，则∠C的度数是（ ）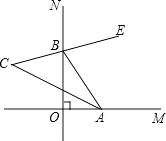

A.30°
B.45°
C.55°
D.60°

Answer 1

【答案】B
【解析】解：根据三角形的外角性质，可得∠ABN=∠AOB+∠BAO，
∵BE平分∠NBA，AC平分∠BAO，
∴∠ABE= ∠ABN，∠BAC= ∠BAO，
∴∠C=∠ABE﹣∠BAC= （∠AOB+∠BAO）﹣ ∠BAO= ∠AOB，
∵∠MON=90°，
∴∠AOB=90°，
∴∠C= ×90°=45°．
故选（B）

根据三角形的一个外角等于与它不相邻的两个内角的和，列式求出∠ABN，再根据角平分线的定义求出∠ABE和∠BAC，然后根据三角形的一个外角等于与它不相邻的两个内角的和，列式计算即可得解．