题目内容

如图，Rt△ABC中，∠C=90°，AC=3，BC=4．建立以A为坐标原点、AB为x轴的平面直角坐标系．求B、C两点的坐标．
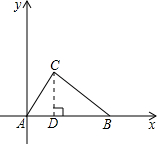
∵∠C=90°，AC=3，BC=4，
∴AB=
AC2+BC2
=5，即B点的坐标为（5，0）．
过C作CD⊥AB于D，则S△ABC=
1
2
AC•BC=
1
2
AB•CD，
∴CD=
AC•BC
AB
=
12
5
，AD=
AC2-CD2
=
9
5
，
∴C点坐标为（
9
5
，
12
5
）．
练习册系列答案
相关题目
如图，四边形ABCD是一正方形，已知A（1，2），B（5，2）
（1）求点C，D的坐标；
（2）若一次函数y=kx-2（k≠0）的图象过C点，求k的值．
（3）若y=kx-2的直线与x轴、y轴分别交于M，N两点，且△OMN的面积等于2，求k的值．
以点P（0，-1）为圆心，3为半径画圆，分别交y轴的正半轴，负半轴于点A，B，则A点坐标为______，B点坐标为______．
若点P（x，y）在第二象限角平分线上，则x与y的关系是______．
已知点A（a+2，a-1）在平面直角坐标系的第四象限内，则a的取值范围为（　　）
A．-2＜a＜1B．-2≤a≤1C．-1＜a＜2D．-1≤a≤2
在平面直角坐标系中，将坐标为（0，0），（2，4），（4，4），（2，0）的点用线段依次连接起来，形成一个图案．问：
（1）若将这四个点的纵坐标保持不变，横坐标变成原来的
1
2
；将所得的四个点用线段依次连接起来，所得图案与原图案相比有什么变化？
（2）纵坐标保持不变，横坐标分别加3呢？
（3）横坐标保持不变，纵坐标分别加3呢？
（4）纵坐标保持不变，横坐标分别乘以-1呢？
（5）横、纵坐标分别变成原来的2倍呢？
（6）横坐标保持不变，纵坐标分别乘以-1呢？
某学校的平面示意图如右所示，如果实验楼所在位置的坐标为（-2，-3），教学楼所在位置的坐标为（-1，2），则图书馆所在位置的坐标为______．
如图，小手盖住的点的坐标可能为（　　）
A．（-4，-6）B．（-6，3）C．（5，2）D．（3，-4）
在直角坐标系中，已知点A（0，2），点P（x，0）为x轴上的一个动点，且线段PA长为3，则x=______．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网