Question

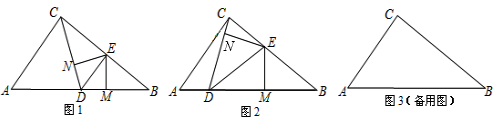
如图1，在Rt△ABC中，∠BAC=90°，AD⊥BC于点D，点O是AC边上一点，连接BO交AD于F，OE⊥OB交BC边于点E．
（1）求证：△ABF∽△COE；
（2）当O为AC的中点，

AC

AB

=2时，如图2，求

OF

OE

的值；
（3）当O为AC边中点，

AC

AB

=n时，请直接写出

OF

OE

的值．

Answer 1

分析：（1）要求证：△ABF∽△COE，只要证明∠BAF=∠C，∠ABF=∠COE即可．
（2）作OH⊥AC，交BC于H，易证△ABF≌△COE，进而证明△ABF∽△HOE，根据相似三角形的对应边的比相等，即可得出所求的值．同理可得（3）

OF

OE

=n．

解答：（1）证明：∵AD⊥BC，
∴∠DAC+∠C=90°．
∵∠BAC=90°，
∴∠BAF=∠C．
∵OE⊥OB，
∴∠BOA+∠COE=90°，
∵∠BOA+∠ABF=90°，
∴∠ABF=∠COE．
∴△ABF∽△COE．

（2）解：过O作AC垂线交BC于H，则OH∥AB，
由（1）得∠ABF=∠COE，∠BAF=∠C．
∴∠AFB=∠OEC，
∴∠AFO=∠HEO，
而∠BAF=∠C，
∴∠FAO=∠EHO，
∴△OEH∽△OFA，
∴OF：OE=OA：OH
又∵O为AC的中点，OH∥AB．
∴OH为△ABC的中位线，
∴OH=

1

2

AB，OA=OC=

1

2

AC，
而

AC

AB

=2，
∴OA：OH=2：1，
∴OF：OE=2：1，即

OF

OE

=2；

（3）解：

OF

OE

=n．

点评：本题难度中等，主要考查相似三角形的判定和性质．