Question

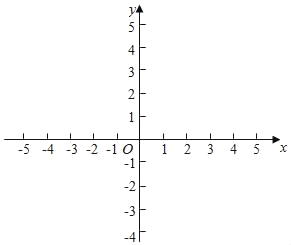
【题目】如图，在平面直角坐标系xOy中，点A的坐标为（﹣2，0），等边三角形AOC经过平移或轴对称或旋转都可以得到△OBD．

（1）△AOC沿x轴向右平移得到△OBD，则平移的距离是 个单位长度；

（2）△AOC与△BOD关于直线对称，则对称轴是 ；

（3）△AOC绕原点O顺时针旋转可以得到△DOB，则旋转角度是 度，在此旋转过程中，△AOC扫过的图形的面积是 ．

Answer 1

【答案】（1）2；（2）y轴；（3）120°, 2π．

【解析】

试题（1）根据平移的性质可以得出△AOC沿x轴向右平移得到△OBD的距离；

（2）△AOC与△BOD关于直线对称，就可以得出△AOC≌△BOD，就有AO=BO，由对称轴的性质就可以得出结论；

（3）根据旋转的性质就可以得出点A与点D是对应点，就可以得出∠AOD就是旋转角，△AOC扫过的面积实际上就是以OA为半径的半圆的面积，由圆的面积公式就可以求出结论．

试题解析：（1）∵A（-2，0），

∴OA=2．

∵△AOC沿x轴向右平移得到△OBD，

∴△AOC≌△OBD，

∴AO=OB，

∴OB=2，

∴平移的距离是2个单位长度．

（2）∵△AOC与△BOD关于直线对称，

∴△AOC≌△BOD，

∴AO=BO．

∴y轴是AB的垂直平分线，

∴对称轴是y轴，

（3）∵△AOC和△OBD都是等边三角形，

∴∠AOC=∠DOB=60°，

∴∠AO=120°，

∴旋转角度是120°．

△AOC扫过的图形的面积是π×22×=2π．

考点: 1.旋转的性质；2.坐标与图形性质；3.轴对称的性质；4.平移的性质．