题目内容
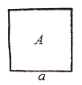
【题目】如图（1），有
、
、
三种不同型号的卡片若干张，其中型是边长为
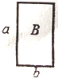
的正方形，型是长为、宽为
的长方形，型是边长为的正方形．
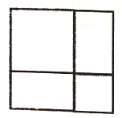
图（1） 图（2）
（1）若用型卡片
张，型卡片
张，型卡片张拼成了一个正方形（如图（2）），此正方形的边长为_______，根据该图形请写出一条属于因式分解的等式：_________；
（2）若要拼一个长为
，宽为
的长方形，设需要类卡片
张，类卡片
张，类卡片
张，则
_______；
（3）现有型卡片张，型卡片
张，型卡片
张，从这
张卡片中拿掉两张卡片，余下的卡片全用上，你能拼出一个长方形或正方形吗？有几种拼法？请你通过运算说明理由．
【答案】（1）a+b，a2+2ab+b2＝（a+b）2；（2）9；（3）（3）四种拼法，理由见解析．
【解析】
（1）由图可得可得正方形的边长为a+b，由图（2）可得因式分解的等式
；
（2）因为
，所以需要用
类卡片2张，
类卡片5张，
类卡片2张，即可求
、
、
对应的值；
（3）分类讨论：第一种：型卡片拿掉1张，型卡片拿掉1张，则能拼出一个长方形，即长方形的长为
，宽为
；第二种：型卡片拿掉1张，型卡片拿掉1张，则能拼出一个长方形，即长方形的长为
，宽为
，此种情况有两种；第三种：型卡片拿掉2张，则能拼出一个正方形方形，即正方形边长为
．
（1）由图（1）和图（2）可得正方形的边长为：a+b，
由图（2）可得因式分解的等式a2+2ab+b2＝（a+b）2．
故答案为a+b，a2+2ab+b2＝（a+b）2；
（2）∵（2a+b）（a+2b）＝2a2+5ab+2b2，
∴需要用A类卡片2张，B类卡片5张，C类卡片2张，
∴x+y+z＝2+5+2＝9；
故答案为9；
（3）四种拼法：理由如下：
第一种：A型卡片拿掉1张，B型卡片拿掉1张，则能拼出一个长方形，即长方形的长为5a+11b，宽为b，
∴
第二种：A型卡片拿掉1张，C型卡片拿掉1张，则能拼出一个长方形，即长方形的长为3a+5b，宽为2b，
∴
；
或者长为6a+10b，宽为b，
，此种情况共2种拼法；
第三种：C型卡片拿掉2张，则能拼出一个正方形方形，即正方形边长为a+3b，
∴
．
