Question

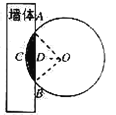
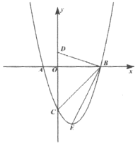
【题目】如图，AB是⊙O的直径，弦BC=4cm，F是弦BC的中点，∠ABC=60°．若动点E以1cm/s的速度从A点出发在AB上沿着A→B运动，设运动时间为t(s)(0≤t＜8)，连接EF，当△BEF是直角三角形时，t(s)的值为________．

Answer 1

【答案】4s或7s

【解析】

先根据直径所对的圆周角是直角可得: ∠ACB=90°,再根据中点定义和锐角三角函数求出BF和AB,然后根据直角的情况分类讨论: ①当∠EFB=90°时,用锐角三角函数求出EB,从而求出AE即可求出t的值; ②当∠BEF=90°时, 用锐角三角函数求出EB,从而求出AE即可求出t的值;

解:∵AB是直径

∴∠ACB=90°

∵弦BC=4cm, F是弦BC的中点，∠ABC=60°

∴BF=BC=2cm,AB==8cm

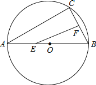
①当∠EFB=90°时,如下图所示,

∴EB==4cm

∴AE=AB－EB=4cm

∴t=AE÷1=4s;

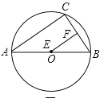
②当∠BEF=90°时,如下图所示,

∴EB==1cm

∴AE=AB－EB=7cm

∴t=AE÷1=7s

综上所述: t(s)的值为4s或7s

故答案为: 4s或7s.