题目内容
如图,直线y=2x与双曲线 在第一象限的交点为A,过点A作AB⊥x轴于B,将△ABO绕点O旋转90°,得到△A′B′O,则点A′的坐标为
在第一象限的交点为A,过点A作AB⊥x轴于B,将△ABO绕点O旋转90°,得到△A′B′O,则点A′的坐标为
| A.(1.0) | B.(1.0)或(﹣1.0) |
| C.(2.0)或(0,﹣2) | D.(﹣2.1)或(2,﹣1) |
D
解析试题分析:联立直线与反比例解析式得: ,
,
消去y得到:x2=1,解得:x=1或﹣1。∴y=2或﹣2。
∴A(1,2),即AB=2,OB=1,
根据题意画出相应的图形,如图所示,分顺时针和逆时针旋转两种情况:
根据旋转的性质,可得A′B′=A′′B′′=AB=2,OB′=OB′′=OB=1,
根据图形得:点A′的坐标为(﹣2,1)或(2,﹣1)。
故选D。

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
下列各点在反比例函数 的图象上的是( )
的图象上的是( )
| A.(-1,-2) | B.(-1,2) | C.(-2,-1) | D.(2,1) |
如图,A是反比例函数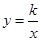 的图像上的一点,AB⊥x轴于点B,且△ABO的面积是3,则k的值是( )
的图像上的一点,AB⊥x轴于点B,且△ABO的面积是3,则k的值是( )
| A.3 | B.-3 | C.-6 | D.6 |
如图,在矩形OABC中,AB=2BC,点A在y轴的正半轴上,点C在x轴的正半轴上,连接OB,反比例函数 (k≠0,x>0)的图象经过OB的中点D,与BC边交于点E,点E的横坐标是4,则k的值是
(k≠0,x>0)的图象经过OB的中点D,与BC边交于点E,点E的横坐标是4,则k的值是
| A.1 | B.2 | C.3 | D.4 |
已知梯形的面积一定,它的高为h,中位线的长为x,则h与x的函数关系大致是
A. | B. | C. | D. |
已知反比例函数的图象经过点(1,2),则此函数图象所在的象限是( )
| A.一、三 | B.二、四 | C.一、三 | D.三、四 |
(2013年四川南充3分)如图,函数 与
与 的图象相交于点A(1,2)和点B,当
的图象相交于点A(1,2)和点B,当 时,自变量x的取值范围是【 】
时,自变量x的取值范围是【 】
| A.x>1 | B.-1<x<0 |
| C.-1<x<0或x>1 | D.x<-1或0<x<1 |
 的图象上,AC边在x轴上,已知∠ACB=90°,∠A=30°,BC=4,则图中阴影部分的面积是
的图象上,AC边在x轴上,已知∠ACB=90°,∠A=30°,BC=4,则图中阴影部分的面积是



 的图象经过点(﹣1,2),则k的值是
的图象经过点(﹣1,2),则k的值是