Question

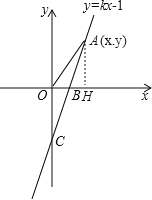
【题目】如图，直线y＝kx－1与x轴、y轴分别交于B、C两点，OB：OC＝.

(1)求B点的坐标和k的值．

(2)若点A(x，y)是第一象限内的直线y＝kx－1上的一个动点，当点A运动过程中，试写出△AOB的面积S与x的函数关系式；

(3)在（2）的条件下，当点A运动到什么位置时，△AOB的面积是.

Answer 1

【答案】（1）B(,0),OB＝ （2）S＝ ,(x＞) （3）A(,)

【解析】

（1）可先求出OC长，并用k的代数式表示点B的坐标及OB的长，然后在△BOC中运用三角函数可求出∠OCB的度数，再运用三角函数就可解决问题．
（2）过点A作AH⊥x轴于H，由于点A在直线y=kx-1上，因此可用x的代数式表示y，进而可得到S与x的函数关系式．
（3）把S=代入（2）中的解析式就可得到点A的横坐标，进而可得到点A的纵坐标．

(1)在Rt△BOC中，

∵ =0，

∴k 1=0.

∴=.

∴点B的坐标为(,0),OB=.

∵=0,∴=01=1.

∴=1.∴OC=1.

∵sin∠OCB=，

∴∠OCB=30°.

∴tan∠OCB=.

∴OB=OC.

∴=×1.

∴k=.

∴B点坐标为(,0),k的值为.

(2)过点A作AH⊥x轴于H，如图.

则有AH=y=x1.x>.

∴S=OBAH=××(x1)= ,(x>).

(3)当S△AOB=时, =.

解得;x=.

∴y=x 1=×1=.

∴点A的坐标为(,).

∴当点A运动到点(,)的位置时,△AOB的面积是.