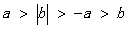题目内容
如图,直线 AB 与 x 轴交于点 A(1,0),与 y 轴交于点 B(0,﹣2).
(1)求直线 AB 的解析式;
若直线 AB 上的点 C 在第一象限,且 S△BOC=2,求点 C 的坐标.
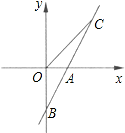
【考点】待定系数法求一次函数解析式.
【专题】计算题.
【分析】(1)设直线 AB 的解析式为 y=kx+b,将点 A(1,0)、点 B(0,﹣2)分别代入解析式即可 组成方程组,从而得到 AB 的解析式;
设点 C 的坐标为(x,y),根据三角形面积公式以及 S△BOC=2 求出 C 的横坐标,再代入直线即可求 出 y 的值,从而得到其坐标.
【解答】解:(1)设直线 AB 的解析式为 y=kx+b(k≠0),
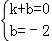 ∵直线 AB 过点 A(1,0)、点 B(0,﹣2),
∵直线 AB 过点 A(1,0)、点 B(0,﹣2),
∴ ,

个体服装店老板以 32 元的价格购进 30 件连衣裙,针对不同的顾客,30 件连衣裙的售价不完全
相同,若以 47 元为标准,将超过的钱数记为正,不足的钱数记为负,记录结果如下表所示:
| 售出件数 | 7 | 6 | 3 | 4 | 5 | |
| 售价/元 | +3 | +2 | +1 | 0 | ﹣1 | ﹣2 |
该服装店在售完这 30 件连衣裙后,赚了多少钱?
某数学兴趣小组再用黑色围棋进行摆放图案的游戏中,小雨同学现已摆放了如下的图案,请根 据图中的信息完成下列的问题.
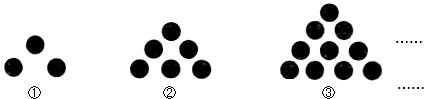
(1)填写下表:
| 图形编号 | ① | ② | ③ | … | … |
| 图中棋子的总数 | 3 | 6 | 10 | … | … |
第 50 个图形中棋子为 1326 颗围棋;
小雨同学如果继续摆放下去,那么第 n 个图案就要用 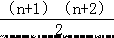 颗围棋;
颗围棋;
(3)如果小雨同学手上刚好有 90 颗围棋子,那么他按照这种规律从第①个图案摆放下去,是否可
以摆放成完整的图案后刚好 90 颗围棋子一颗不剩?如果可以,那么刚好摆放完成几个完整的图案? 如果不行,那么最多可以摆放多少个完整图案,还剩余几颗围棋子?(只答结果,不说明理由)
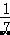 、
、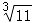 、0.3333、
、0.3333、 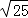 、
、 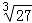 、0.5757757775…、﹣
、0.5757757775…、﹣ 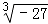 、中,其中无理数有 个.
、中,其中无理数有 个.
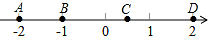
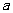 、
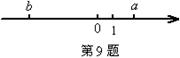
、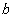 在数轴上的对应点的位置如图所示,则
在数轴上的对应点的位置如图所示,则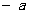 、
、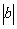 的大小关系正确的是
的大小关系正确的是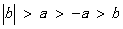 B.
B. 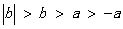
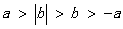 D.
D.