题目内容
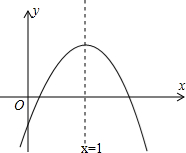已知抛物线y=ax2+bx+c（a≠0）的图象如图所示，下列结论：（1）abc＞0；（2）b＞0；（3）4a+2b+c＞0；（4）（a+b）2＜b2，其中正确的有______（把所有正确的结论的序号填出来）
解：根据图象可得：a＜0，c＜0，
∵对称轴为x=1，即-
=1，
∴可得b＞0，即（2）正确；
∴abc＞0，即（1）正确；
函数的对称轴为x=1，则结合图象可得
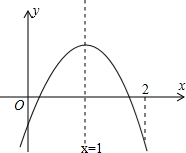
当x=2时，y＜0，即4a+2b+c＜0，即可得（3）错误；
∵a＜0，b＞0，
∴|a+b|＜|b|，
∴（a+b）2＜b2，即可得（4）正确．
故答案为：（1）（2）（4）．
分析：根据函数图象可得a＜0，c＜0，再由对称轴为x=1，可得出b＞0，从而可判断（1）（2），再由对称轴为x=1，可得出当x=2时，y＜0，从而判断出（3），判断出|a+b|与|b|的大小可判断出（4）．
点评：本题考查了二次函数图象与系数的关系，根据图象与y轴的交点可判断出c，根据抛物线的开口可判断出a，要求熟练掌握抛物线的对称性及对称轴表达式．
∵对称轴为x=1，即-
=1，∴可得b＞0，即（2）正确；
∴abc＞0，即（1）正确；
函数的对称轴为x=1，则结合图象可得
当x=2时，y＜0，即4a+2b+c＜0，即可得（3）错误；
∵a＜0，b＞0，
∴|a+b|＜|b|，
∴（a+b）2＜b2，即可得（4）正确．
故答案为：（1）（2）（4）．
分析：根据函数图象可得a＜0，c＜0，再由对称轴为x=1，可得出b＞0，从而可判断（1）（2），再由对称轴为x=1，可得出当x=2时，y＜0，从而判断出（3），判断出|a+b|与|b|的大小可判断出（4）．
点评：本题考查了二次函数图象与系数的关系，根据图象与y轴的交点可判断出c，根据抛物线的开口可判断出a，要求熟练掌握抛物线的对称性及对称轴表达式．
练习册系列答案
相关题目
与x轴的另一个交点为E．
如图，已知抛物线y=ax2+bx+c（其中b＞0，c＜0）的顶点P在x轴上，与y轴交于点Q，过坐标原点O，作OA⊥PQ，垂足为A，且OA=