题目内容
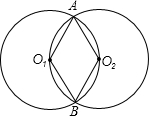 如图,圆O1与圆O2相交于A、B两点,它们的半径都为2,圆O1经过点O2,则四边形O1AO2B的面积为
如图,圆O1与圆O2相交于A、B两点,它们的半径都为2,圆O1经过点O2,则四边形O1AO2B的面积为分析:连接O1O2,由题意知,四边形AO1BO2B是菱形,且△AO1O2,△BO1O2都是等边三角形,四边形O1AO2B的面积等于两个等边三角形的面积.据此求四边形O1AO2B的面积.
解答: 解:连接O1O2,由题意知,四边形AO1BO2B是菱形,且△AO1O2,△BO1O2都是等边三角形,四边形O1AO2B的面积等于两个等边三角形的面积,
解:连接O1O2,由题意知,四边形AO1BO2B是菱形,且△AO1O2,△BO1O2都是等边三角形,四边形O1AO2B的面积等于两个等边三角形的面积,
∴SO1AO2B=2×
×2×2×sin60°=2
.
 解:连接O1O2,由题意知,四边形AO1BO2B是菱形,且△AO1O2,△BO1O2都是等边三角形,四边形O1AO2B的面积等于两个等边三角形的面积,
解:连接O1O2,由题意知,四边形AO1BO2B是菱形,且△AO1O2,△BO1O2都是等边三角形,四边形O1AO2B的面积等于两个等边三角形的面积,∴SO1AO2B=2×
| 1 |
| 2 |
| 3 |
点评:本题利用了等边三角形判定和性质,等边三角形的面积公式求解.

练习册系列答案
相关题目
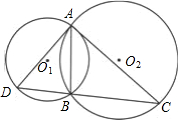 如图,圆O1与圆O2相交于A、B,过A作圆O1的切线交圆O2于C,连CB并延长交圆O1于D,连AD,AB=2,BD=3,BC=5,则AD的长为( )
如图,圆O1与圆O2相交于A、B,过A作圆O1的切线交圆O2于C,连CB并延长交圆O1于D,连AD,AB=2,BD=3,BC=5,则AD的长为( )A、
| ||||
B、
| ||||
C、
| ||||
D、2
|
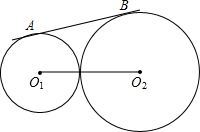 如图,圆O1与圆O2相外切,两圆半径分别为2和3,则两圆公切线AB长为( )
如图,圆O1与圆O2相外切,两圆半径分别为2和3,则两圆公切线AB长为( )A、2
| ||
B、
| ||
C、2
| ||
D、2
|
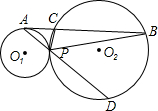 线AP交圆O2于点D,连接DC、PC.
线AP交圆O2于点D,连接DC、PC.