Question

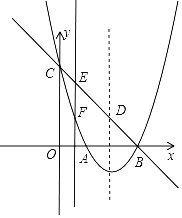
【题目】如图，抛物线的对称轴为，与轴的一个交点在和之间，其部分图象如图所示，则下列结论：（1）：（2）；（3）（为任意实数）；（4）；5）点是该抛物线上的点，且，其中正确结论的个数是（ ）

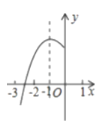
A. 2B. 3C. 4D. 5

Answer 1

【答案】C

【解析】

根据抛物线的增减性、对称轴及抛物线与x轴交点情况进行推理，进而对所得结论进行判断．

（1）由抛物线与轴有两个不同的交点知，.故正确；

（2）由抛物线的对称轴是直线知，，则，故正确；

（3）∵，∴方程中，

∴抛物线与轴只有一个交点，

∵图中抛物线开口向下，∴，∴，

即.∴（为任意实数）故正确；

（4）∵当时，，且，

∴，∴，故正确；

（5）：①∵抛物线的对称轴为，点在抛物线上，

∴根据抛物线的对称性质知：.

∵，且抛物线对称轴左边图象值随的增大而增大，

∴.故错误；综上所述，正确的结论有4个.

故选：C.