Question

【题目】如图，矩形纸片中，已知，，点在边上，沿折叠纸片，使点落在点处，连结，当为直角三角形时，的长为______.

Answer 1

【答案】3或

【解析】

分两种情况：①当∠EFC=90°，先判断出点F在对角线AC上，利用勾股定理求出AC，设BE=x,表示出CE，根据翻折变换的性质得到AF=AB,EF=BE，再根据Rt△CEF利用勾股定理列式求解；②当∠CEF=90°，判断四边形ABEF是正方形，根据正方形的性质即可求解.

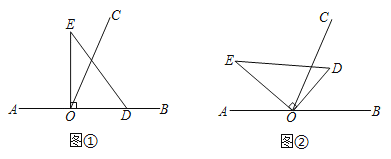
分两种情况：①当∠EFC=90°，如图1，

∵∠AFE=∠B=90°，∠EFC=90°，

∴点A、F、C共线，

∵矩形ABCD的边AD=4，

∴BC=AD=4，

在Rt△ABC中，AC=

设BE=x，则CE=BC-BE=4-x，

由翻折的性质得AF=AB=3,EF=BE=x，∴CF=AC-AF=5-3=2

在Rt△CEF中，EF2+CF2=CE2，

即x2+22=(4-x)2，

解得x=；

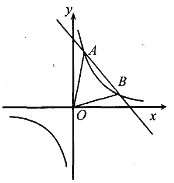
②当∠CEF=90°，如图2

由翻折的性质可知∠AEB=∠AEF=45°，

∴四边形ABEF是正方形，

∴BE=AB=3，

故BE的长为3或