题目内容
解:x+ =1,
=1,
移项,得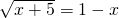 ,
,
x+5=x2-2x+1,
整理,得x2-3x-4=0,
(x-4)(x+1)=0,
解得x1=4,x2=-1,
∴经检验x1=4是增根,舍去
∴x2=-1是原方程的解.
分析:观察原方程可经过以下几步求解:
①首先应通过移项使方程的左边只含有一个代根号的式子;
②再两边平方消去根号;
③整理该方程将方程的右边化为0、并将整理后的方程左边分解为两个一次因式的乘积;
④最后令每个因式分别等于零,得到两个一元一次方程,解该一元一次方程即可求出原方程的解.
点评:本题主要考查运用“因式分解”的方法解一元二次方程的能力,首先应将方程的右边化为0,对于方程的左边通过因式分解分解成两个一次因式的乘积.如果两因式相乘的乘积为0,那么这两个因式中至少有一个为0,依此将原方程等价于求两个一元一次方程的解.另外对于分式方程和带有根号的方程求出的解应注意检验是否是增根.
 =1,
=1,移项,得
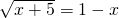 ,
,x+5=x2-2x+1,
整理,得x2-3x-4=0,
(x-4)(x+1)=0,
解得x1=4,x2=-1,
∴经检验x1=4是增根,舍去
∴x2=-1是原方程的解.
分析:观察原方程可经过以下几步求解:
①首先应通过移项使方程的左边只含有一个代根号的式子;
②再两边平方消去根号;
③整理该方程将方程的右边化为0、并将整理后的方程左边分解为两个一次因式的乘积;
④最后令每个因式分别等于零,得到两个一元一次方程,解该一元一次方程即可求出原方程的解.
点评:本题主要考查运用“因式分解”的方法解一元二次方程的能力,首先应将方程的右边化为0,对于方程的左边通过因式分解分解成两个一次因式的乘积.如果两因式相乘的乘积为0,那么这两个因式中至少有一个为0,依此将原方程等价于求两个一元一次方程的解.另外对于分式方程和带有根号的方程求出的解应注意检验是否是增根.

练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目
若(x+1)2+
=0,则x+y的值为( )
| 2y-1 |
| A、-1 | ||
B、
| ||
| C、0 | ||
D、-
|

